If your pre-calculus teacher asks you to find the value of an infinite sum in a geometric sequence, the process is actually quite simple — as long as you keep your fractions and decimals straight. If r lies outside the range –1 r 1, an grows without bound infinitely, so there's no limit on how large the absolute value of an (|an|) can get. If |r| n, |rn| continues to decrease infinitely until it becomes arbitrarily close to 0. This decrease is because when you multiply a fraction between –1 and 1 by itself, the absolute value of that fraction continues to get smaller until it becomes so small that you hardly notice it. Therefore, the term rk almost disappears completely in the finite geometric sum formula:
And if the rk disappears — or gets very small — the finite formula changes to the following and allows you to find the sum of an infinite geometric series:
For example, follow the steps to find this value:
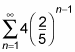
Find the value of a1 by plugging in 1 for n.

Calculate a2 by plugging in 2 for n.

Determine r.
To find r, you divide a2 by a1:

Plug a1 and r into the formula to find the infinite sum.
Plug in and simplify to find the following:

Repeating decimals also can be expressed as infinite sums. Consider the number 0.5555555. . . . You can write this number as 0.5 + 0.05 + 0.005 + . . . , and so on forever. The first term of this sequence is 0.5; to find r, 0.05 divided by 0.5 = 0.1.
Plug these values into the infinite sum formula:
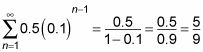
Keep in mind that this sum is finite only if r lies strictly between –1 and 1.





