The Taylor series provides a template for representing a wide variety of functions as power series. It is relatively simple to work with, and you can tailor it to obtain a good approximation of many functions.
Here’s the Taylor series in all its glory:
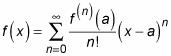
The Taylor series uses the notation f(n) to indicate the nth derivative. Here’s the expanded version of the Taylor series:
The presence of the variable a provides the Taylor series with a lot of flexibility, as the next example illustrates.
Suppose you want to approximate the value of sin 10. You can use only four terms of the Taylor series to make a good approximation. The key to this approximation is a shrewd choice for the variable a:
Let a = 3
This choice has two advantages: First, this value of a is close to 10 (the value of x), which makes for a good approximation. Second, it’s an easy value for calculating sines and cosines, so the computation shouldn’t be too difficult.
To start off, substitute 10 for x and 3 for a in the first four terms of the Taylor series:
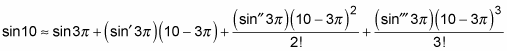
Next, substitute in the first, second, and third derivatives of the sine function and simplify:
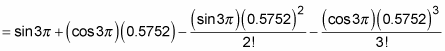
The good news is that sin 3 = 0, so the first and third terms fall out:
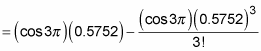
At this point, you probably want to grab your calculator:
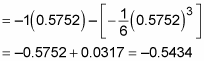
This approximation is correct to two decimal places.





