The Park test begins by assuming a specific model of the heteroskedastic process. Specifically, it assumes that the heteroskedasticity may be proportional to some power of an independent variable (Xk) in the model. This assumption can be expressed as
You can obtain a linearized version of the Park model by using a log transformation:
Because the values for
aren’t known in practice, your
are calculated from the residuals and used as proxies for
Most econometrics software programs don’t have commands that allow you to automatically perform a Park test. However, you can perform the test by following these steps:
Estimate the model using OLS:

Obtain the squared residuals, after estimating your model:
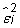
Estimate the model using OLS:
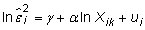
Examine the statistical significance of alpha using the t-statistic:

The value of
from estimating the regression
is an estimate of the constant (homoskedastic) portion of the error variance. Consequently, if the estimate of the alpha coefficient is statistically significant, then you have evidence of heteroskedasticity. If not, you fail to reject the null hypothesis of homoskedasticity.
Using data from Major League Baseball players, you can estimate a model with the natural log of the player’s contract value as the dependent variable and several player characteristics as independent variables.
The independent variables include three-year averages for the player’s slugging percentage (slg_3_avg) and at-bats (ab_3_avg), the player’s age, and the player’s tenure (years) with the current team. The figure illustrates the step-by-step process of performing a Park test in STATA.
If there’s heteroskedasticity, then at-bats is the variable responsible for it. In this case, the coefficient for the variable lnabavg (using the natural log of ab_3_avg as specified by the Park test) is statistically significant with a p-value of 0.03. Therefore, you can reject the hypothesis of homoskedasticity.
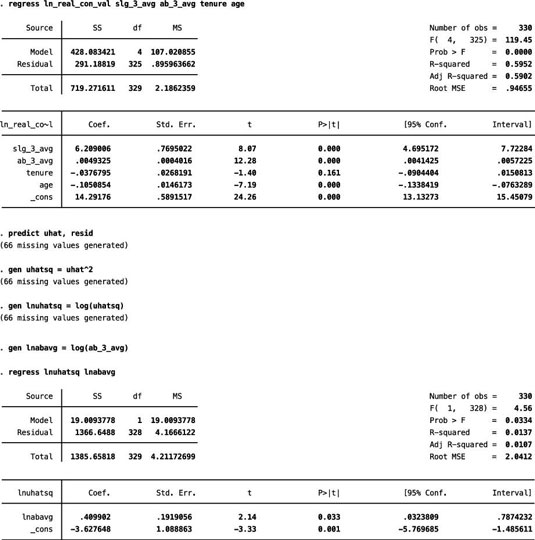
The Park test’s weakness is that it assumes the heteroskedasticity has a particular functional form. Furthermore, identifying heteroskedasticity with one independent variable doesn’t rule out the fact that other variables may also play a role.
Although discussions of the Park test are still common in many econometrics textbooks, applied econometricians typically rely on other alternatives to test for heteroskedasticity, such as the Breusch-Pagan or White tests.





