Find the Zero-State Response of a Parallel RL Circuit

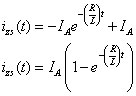
After fiddling with the math, you determine that the zero-input response of the sample circuit is this:

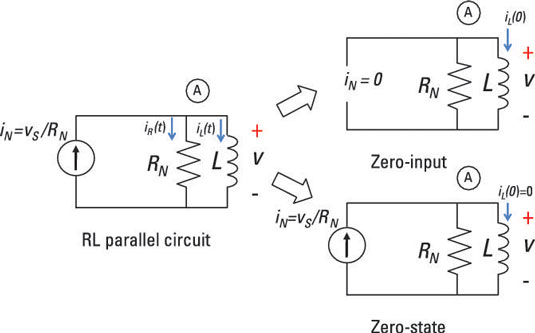
Now you are ready to calculate the zero-state response for the circuit. Zero-state response means zero initial conditions. For the zero-state circuit shown earlier, zero initial conditions means looking at the circuit with zero inductor current at t < 0. You need to find the homogeneous and particular solutions to get the zero-state response.

Next, you have zero initial conditions and an input current of i_N(t) = u(t), where u(t) is a unit step input.

When the step input u(t) = 0, the solution to the differential equation is the solution i_h(t):

The inductor current i_h(t) is the solution to the homogeneous first-order differential equation:

This solution is the general solution for the zero input. You find the constant c₁ after finding the particular solution and applying the initial condition of no inductor current.

After time t = 0, a unit step input describes the transient inductor current. The inductor current for this step input is called the step response.

You find the particular solution i_p(t) by setting the step input u(t) equal to 1. For a unit step input i_N(t) = u(t), substitute u(t) = 1 into the differential equation:

The particular solution i_p(t) is the solution for the differential equation when the input is a unit step u(t) = 1 after t = 0. Because u(t) = 1 (a constant) after time t = 0, assume a particular solution i_p(t) is a constant I_A.

Because the derivative of a constant is 0, the following is true:

Substitute i_p(t) = I_A into the first-order differential equation:

The particular solution eventually follows the form of the input because the zero-input (or free response) diminishes to 0 over time. You can generalize the result when the input step has strength I_A or I_Au(t).

You need to add the homogeneous solution i_h(t) and the particular solution i_p(t) to get the zero-state response:

At t = 0, the initial condition is 0 because this is a zero-state calculation. To find c₁, apply i_ZS(0) = 0:

Solving for c₁ gives you

C₁ = -I_A