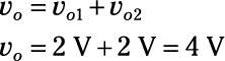Analyze Circuits with Two Independent Sources Using Superposition

Use superposition to analyze circuits that have lots of voltage and current sources. Superposition helps you to break down complex linear circuits composed of multiple independent sources into simpler circuits that have just one independent source. The total output, then, is the algebraic sum of individual outputs from each independent source.

Analyze circuits with two voltage sources

With the help of superposition, you can break down the complex circuit shown here into two simpler circuits that have just one voltage source each. To turn off a voltage source, you replace it with a short circuit.

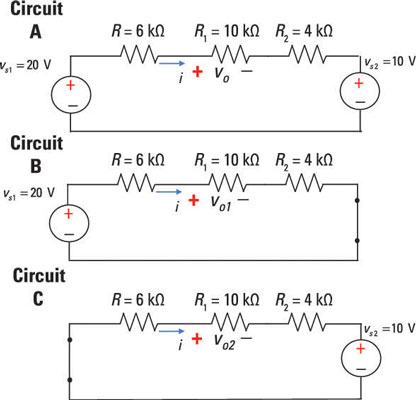
Circuit A contains two voltage sources, v_s1 and v_s2, and you want to find the output voltage v_o across the 10-kΩ resistor. The next diagram shows the same circuit with one voltage source turned off: Circuit B contains one voltage source, with v_s2 turned off and replaced by a short circuit. The output voltage due to v_s1 is v_o1.

Similarly, Circuit C is Circuit A with the other voltage source turned off. Circuit C contains one voltage source, with v_s1 replaced by a short circuit. The output voltage due to voltage source v_s2 is v_o2.

Summing up the two outputs due to each voltage source, you wind up with the following output voltage:

To find the output voltages for Circuits B and C, you use voltage divider techniques. That is, you use the idea that a circuit with a voltage source connected in series with resistors divides its source voltage proportionally according to the ratio of a resistor value to the total resistance.

In Circuit B, you simply find the output voltage v_o1 due to v_s1 with a voltage divider equation:

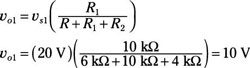
In Circuit C, finding the output voltage v_o2 due to v_s2 also requires a voltage divider equation, with the polarities of v_o2 opposite v_s2. Using the voltage divider method produces the output voltage v_o2 as follows:

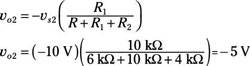
Adding up the individual outputs due to each source, you wind up with the following total output for the voltage across the 10-kΩ resistor:

When the sources are two current sources

The plan in this section is to reduce the circuit shown here to two simpler circuits, each one having a single current source, and add the outputs using superposition.

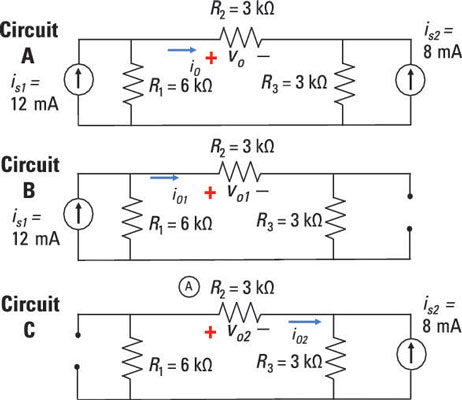
You consider the outputs from the current sources one at a time, turning off a current source by replacing it with an open circuit.

Circuit A consists of two current sources, i_s1 and i_s2, and you want to find the output current i_o flowing through resistor R₂. Circuit B is the same circuit with one current source turned off: Circuit B contains one current source, with i_s2 replaced by an open circuit. The output voltage due to i_s1 is i_o1.

Similarly, Circuit C is Circuit A with only current source, with i_s1 replaced by an open circuit. The output current due to current source i_s2 is i_o2.

Adding up the two current outputs due to each source, you wind up with the following net output current through R₂:

To find the output currents for Circuits B and C, you use current divider techniques. That is, you use the idea that for a parallel circuit, the current source connected in parallel with resistors divides its supplied current proportionally according to the ratio of the value of the conductance to the total conductance.

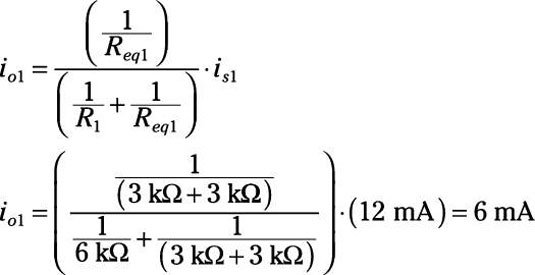
For Circuit B, you find the output current i_o1 due to i_s1 using a current divider equation. Note that there are two 3-kΩ resistors connected in series in one branch of the circuit, so use their combined resistance in the equation. Given R_eq1 = 3 kΩ + 3 kΩ and R₁ = 6 kΩ, here’s output current for the first current source:

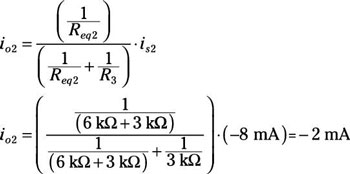
In Circuit C, the output current i_o2 due to i_s2 also requires a current divider equation. Note the current direction between i_o2 and i_s2: i_s2is opposite in sign to i_o2. Given R_eq2 = 6 kΩ + 3 kΩ and R₃ = 3 kΩ, the output current from the second current source is

Adding up i_o1 and i_o2, you wind up with the following total output current:

When there is one voltage source and one current source

You can use superposition when a circuit has a mixture of two independent sources, with one voltage source and one current source. You need to turn off the independent sources one at a time. To do so, replace the current source with an open circuit and the voltage source with a short circuit.

Circuit A of the sample circuit shown here has an independent voltage source and an independent current source. How do you find the output voltage v_o as the voltage across resistor R₂?

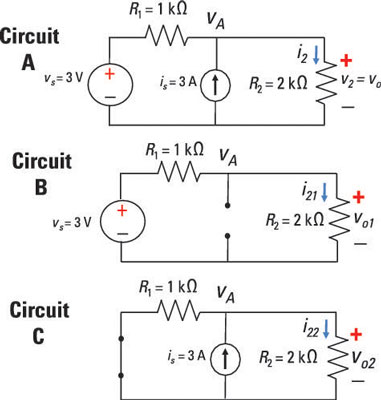
Circuit A (with its two independent sources) breaks up into two simpler circuits, B and C, which have just one source each. Circuit B has one voltage source because the current source was replaced with an open circuit. Circuit C has one current source because the voltage source was replaced with a short circuit.

For Circuit B, you can use the voltage divider technique because its resistors, R₁ and R₂, are connected in series with a voltage source. So here’s the voltage v_o1 across resistor R₂:

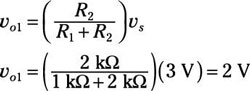
For Circuit C, you can use a current divider technique because the resistors are connected in parallel with a current source. The current source provides the following current i₂₂ flowing through resistor R₂:

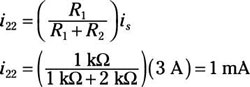
You can use Ohm’s law to find the voltage output v_o2 across resistor R₂:

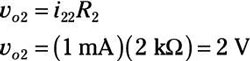
Now find the total output voltage across R₂for the two independent sources in Circuit C by adding v_o1 (due to the source voltage v_s) and v_o2 (due to the source current i_s). You wind up with the following output voltage: