You can use calculus and the Lagrangian function in managerial economics to maximize utility. Remember, utility is the amount of satisfaction an individual receives from consuming a good.
How to measure consumer indifference
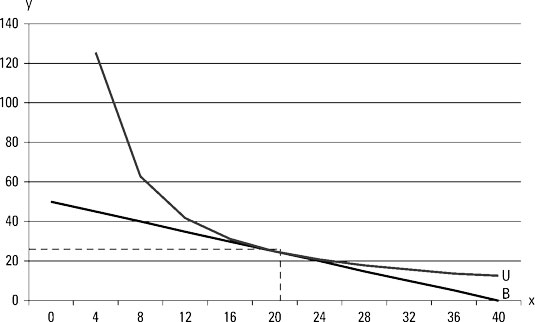
Indifference exists when the amount of utility a customer gets in one situation exactly equals the amount of utility that customer gets in another situation. Indifference curves can be described by functions. For example
shows the relationship between the quantity consumed of good x, the quantity consumed of good y, and total utility.
How to measure constraining factors
Again, consumers face a budget constraint. For example, a consumer has a weekly budget of $400 for goods x and y. The price of good x is $10 and the price of good y is $8. The budget constraint is
where x and y are the quantities consumed of each good.
Lagrangians can make you happy
You’ll recognize this as a constrained optimization problem — the consumer is trying to maximize utility, subject to a budget constraint. This situation is ideal for a Lagrangian.
The consumer wants to maximize utility, subject to the budget constraint, based upon the Lagrangian functions. The steps you take in order to determine the quantity of x and y that maximize utility are the following:
Create a Lagrangian function. Recognize that the variable you’re trying to maximize is total utility. So, your objective function is 8x0.5y0.5. Second, your constraint is represented by the budget 400 – 10x – 8y = 0. Your Lagrangian function Â’ is

Take the partial derivative of the Lagrangian with respect to x and y, the commodities you’re consuming, and set them equal to zero. These equations ensure that total utility is being maximized.

Take the partial derivative of the Lagrangian function with respect to ë and set it equal to zero. This partial derivative ensures that the budget constraint is satisfied.
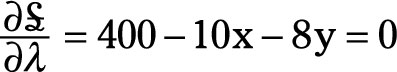
Solving the three partial derivatives simultaneously for the variables x, y, and λ maximizes total utility, subject to the budget constraint.
Rewriting the partial derivative of Β’ with respect to x enables you to solve for λ.
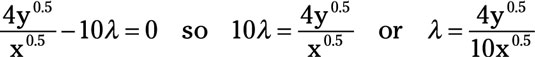
Substituting the above equation for λ in the partial derivative of Β’ with respect to y yields
So
Finally, substituting 0.8y for x in the constraint (the partial derivative of Β’ with respect to λ) yields
Thus, you should consume 25 units of good y.
Earlier you determined x = 0.8y.
Finally, you can solve for λ.
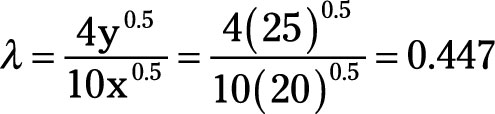
Therefore, the combination 20 units of good x and 25 units of good y maximizes total utility given the budget constraint.
In addition, λ equals 0.447. Lambda is an awesome shortcut. Most decisions are affected by constraints, but constraints are not necessarily absolute. Often times, a constraint can be varied a little bit. Lambda, the Lagrangian multiplier, shows you the impact changing the constraint has on the objective function.
Specifically, if you change the constraint one unit, lambda indicates how much the variable you’re optimizing will change. Thus, in the example, if your income increases by $1 (you change the constraint by one unit) your total utility increases by 0.447 utils.