To maximize profit by using marginal revenue and marginal cost, you focus on the contribution one additional unit of output makes to your revenue relative to its contribution to your cost.
Marginal revenue is the change in total revenue that occurs when one additional unit of output is produced. Thus,

This equation indicates that marginal revenue is the slope of the total revenue function.
Marginal cost is the change in total cost that occurs when one additional unit of output is produced.

So, marginal cost is the slope of the total cost equation.
In order to maximize profit, you want to maximize the difference between total revenue and total cost. Thus, if your marginal revenue is greater than your marginal cost (MR>MC), an additional unit of output adds more to your firm’s revenue than it adds to your firm’s cost, and the additional unit earns you more profit.
On the other hand, if your marginal revenue is less than your marginal cost (MR In order to maximize profit, you want to produce the quantity of output that corresponds to marginal revenue equals marginal cost (MR=MC). The illustration indicates the profit-maximizing quantity of output by using marginal revenue equals marginal cost. The marginal revenue curve is horizontal because you can sell every unit you produce at the prevailing market price. Thus, price equals marginal revenue or This equation also represents the firm’s demand curve, d, because if the firm charges a price one cent higher than P nobody will buy its product and the quantity demanded equals zero. However at the price P, the firm can sell everything it produces. The firm’s marginal cost curve is eventually upward-sloping, passing through the minimum points on the average-variable-cost and average-total-cost curves. The output level where marginal revenue and marginal cost intersect, q0, is the profit-maximizing quantity of output. This output level is exactly the same as the output level q0 determined by using total revenue and total cost. Because marginal revenue represents the slope of the total revenue function and marginal cost represents the slope of the total cost function, profit is maximized at the output level where the slopes of total revenue and total cost are the same. Regardless of whether you maximize profit using total revenue and total cost or marginal revenue and marginal cost, you get the same answer for the profit-maximizing quantity of output. If your firm produces output at a level less than q0, such as qA, those units add more to your revenue than they add to your cost because marginal revenue is greater than marginal cost. Those units, by adding more to your revenue than they add to your cost, cause your profit to increase. Therefore, you want to increase production and move toward q0. If your firm produces output beyond q0, say qB, those units add more to your cost than they add to your revenue because marginal cost for those units is greater than marginal revenue. By adding more to your cost than they add to your revenue, those units cause your profit to be lower. So, you want to decrease production and move back toward q0.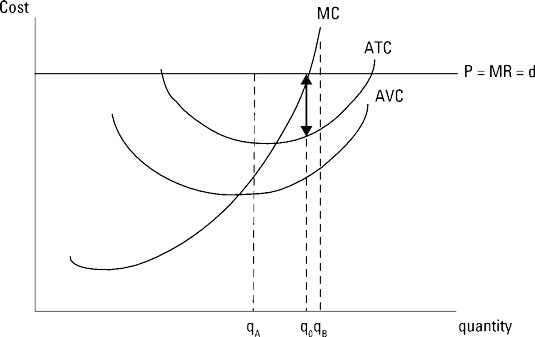
![]()





