How to Work with Radicals and Absolute Value on the PSAT/NMSQT

On the PSAT/NMSQT math sections, you may run across radicals and absolute values. You’ll have to know how to treat them when you apply PEMDAS (the order of operations pneumonic that you should have memorized— parentheses, exponents, multiply, divide, add, subtract).

A radical is a square root, the number that, multiplied by itself, gives you the number under the radical. The

is 8, because 8 x 8 = 64.

You may also find an absolute value (a number placed inside two parallel lines, which represents either the positive or the negative form of the number). Remember these rules when you hit a radical or absolute value:

• You can multiply and divide radicals. So

  

  The numbers don’t change, just because they have that cute little tent-like symbol over them.

• You can add or subtract radicals only when they match. It’s legal to subtract

  

• To add or subtract unlike radicals, factor out a perfect square so that the radicals match. Say you’re trying to add

  

  Mismatch!

  

  In the same way, you can factor

  

  Okay, now you’re adding

  

  Don’t forget that when two negative numbers are multiplied, the result is positive. That means, for example, that 3² and (–3)² both equal 9.

• Treat radicals like parentheses, in the order of operations. Simplify anything inside of the radical, deal with the radical, and then move on.

• Treat absolute values like parentheses, in the order of operations. In other words, compute the absolute value before you work the rest of the problem. You can recognize absolute value because the number appears to be lying between two train tracks, like this: |11|.

  You can have a few things inside the train tracks, like this: |2 – 5|. If you can simplify an absolute value, do so before doing anything else. So change |2 – 5| to | –3|. After you simplify, change whatever’s on the train tracks to positive 3.

Don’t change the absolute value to positive until you’ve simplified it. Do the math inside the train tracks first, and then change the answer to positive.

Here’s a radical suggestion: Try these practice problems.

1. Simplify:

   

   (A) –2

   (B) 2

   (C) 6

   (D) 12

   (E) 16

2. The following expression is equivalent to which choice?

   

   (A) 8

   (B) [neq07046]

   (C) [neq07047]

   (D) [neq07048]

   (E) [neq07049]

3. Simplify the following expression:

   
   

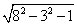
Now check your answers:

1. B.

   Deal with the radical first: 5 + 2² requires you to square 2 before adding it to 5, so you get 5 + 4 = 9, which becomes 3 when you apply the square root. Your expression now looks like 3 – |2 – 7| + 4; time to tackle the absolute value part.

   You know that 2 – 7 = –5, but the absolute value sign turns that into a positive 5. Your expression is now 3 – 5 + 4, or 2, Choice (B).

2. C.

   Absolute value inside of a radical?! Take it one step at a time. The absolute value needs to be handled before you can even think about the radical, so start there. |2 – 5| = |–3| = 3, so you can rewrite the expression as follows when you simplify inside of the radical.

   

   Unfortunately, 12 isn’t a perfect square, but it does have 4 as a factor. You can rewrite:

   

3. B.

   Simplify everything inside the radical first, beginning with exponents: 8² – 3² – 1 = 64 – 9 – 1 = 54. Now, see if you can split 54 up so that it is the product of a perfect square and another number: 54 = 9 x 6. Put that back inside the radical, and you find that