The coordinate plane doesn’t have wings, but it does have points that spread out infinitely. You may not have encountered the coordinate plane in a while (it isn’t something most people deal with in everyday life), so take just a minute to refresh your memory about a few relevant terms that may pop up on the GMAT. Although you won’t be asked to define the terms related to the coordinate plane, knowing what they mean is absolutely essential to answering GMAT math questions.
Line dancing: Understanding coordinate geometry
Before you get too engrossed in the study of coordinate geometry, ground yourself with an understanding of these essential terms:
- Coordinate plane: The coordinate plane is a perfectly flat surface where points can be identified by their positions, using ordered pairs of numbers. These pairs of numbers represent the points’ distances from an origin on perpendicular axes. The coordinate of any particular point is the set of numbers that identifies the location of the point, such as (3, 4) or (x, y).
- x-axis: The x-axis is the horizontal axis (number line) on a coordinate plane. The values start at the origin, which has a value of 0. Numbers increase in value to the right of the origin and decrease in value to the left. The x value of a point’s coordinate is listed first in its ordered pair.
- y-axis: The y-axis is the vertical axis (number line) on a coordinate plane. Its values start at the origin, which has a value of 0. Numbers increase in value going up from the origin and decrease in value going down. The y value of a point’s coordinate is listed second in its ordered pair.
- Origin: The origin is the point (0, 0) on the coordinate plane. It’s where the x- and y-axes intersect.
- Ordered pair: Also known as a coordinate pair, this duo is the set of two values that expresses the distance a point lies from the origin. The horizontal (x) coordinate is always listed first, and the vertical (y) coordinate is listed second.
- x-intercept: The value of x where a line, curve, or some other function crosses the x- The value of y is 0 at the x-intercept. The x-intercept is often the solution or root of an equation.
- y-intercept: The value of y where a line, curve, or some other function crosses the y- The value of x is 0 at the y-intercept.
- Slope: Slope measures how steep a line is and is commonly referred to as the rise over the run.
What’s the point? Finding the coordinates
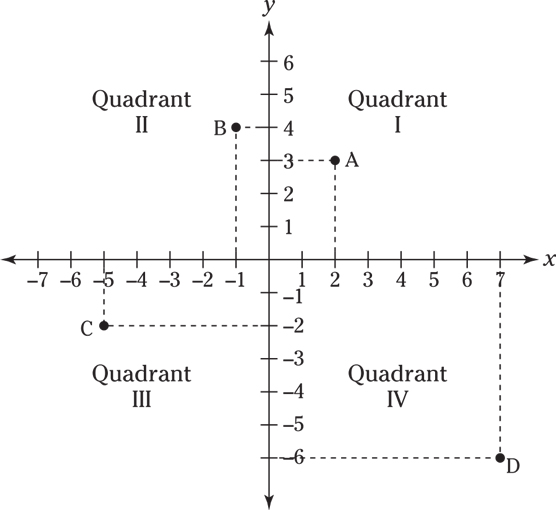
You can identify any point on the coordinate plane by its coordinates, which designate the point’s location along the x- and y-axes. For example, the ordered pair (2, 3) has a coordinate point located two units to the right of the origin along the horizontal (x) number line and three units up on the vertical (y) number line. In the figure, point A is at (2, 3). The x-coordinate appears first, and the y-coordinate shows up second. Pretty simple so far, huh?
Points on the coordinate plane
On all fours: Identifying quadrants
The intersection of the x- and y-axes forms four quadrants on the coordinate plane, which just so happen to be named Quadrants I, II, III, and IV. Here’s what you can assume about points based on the quadrants they’re in:
- All points in Quadrant I have a positive x value and a positive y.
- All points in Quadrant II have a negative x value and a positive y.
- All points in Quadrant III have a negative x value and a negative y.
- All points in Quadrant IV have a positive x value and a negative y.
- All points along the x-axis have a y value of 0.
- All points along the y-axis have an x value of 0.
Quadrant I starts to the right of the y-axis and above the x-axis. It’s the upper-right portion of the coordinate plane. As shown in Figure 18-1, the other quadrants move counterclockwise around the origin. The figure also shows the location of coordinate points A, B, C, and D:
- Point A is in Quadrant I and has coordinates (2, 3).
- Point B is in Quadrant II and has coordinates (–1, 4).
- Point C is in Quadrant III and has coordinates (–5, –2).
- Point D is in Quadrant IV and has coordinates (7, –6).
The GMAT won’t ask you to pick your favorite quadrant, but you may be asked to identify which quadrant a particular point belongs in.
