What Happens to a Wave Function When You Swap Two Particles

When you swap the order of operations for two particles in a multi-particle atom, this affects their wave function. Whether the wave function is symmetric under such operations gives you insight into whether the two particles can occupy the same quantum state.

Take a look at the general wave function for N particles:

In this case, you can think of symmetry in terms of the location coordinate, r, to keep things simple, but you can also consider other quantities, such as spin, velocity, and so on. That wouldn’t make this discussion any different, because you can wrap all of a particle’s quantum measurements — location, velocity, speed, and so on — into a single quantum state, which you can call

Doing so would make the general wave function for N particles into this:

But this example just considers the wave function

to keep things simple.

Now imagine that you have an exchange operator, P_ij, that exchanges particles i and j. In other words,

And P_ij = P_ji, so

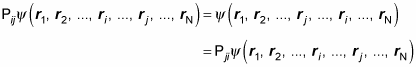
Also, note that applying the exchange operator twice just puts the two exchanged particles back where they were originally, so

Here’s what that looks like:

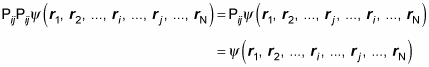
However, in general, P_ij and P_lm

do not commute. That is,

Therefore,

For example, say you have four particles whose wave function is

Apply the exchange operators P₁₂ and P₁₄ to see whether P₁₂ P₁₄ equals P₁₄ P₁₂. Here’s

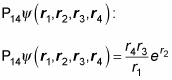
And here’s what

looks like:

Okay. Now take a look at

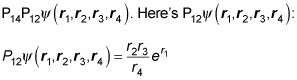
And here’s what

looks like:

As you can see by comparing

and this last equation,

In other words, the order in which you apply exchange operators matters.