In quantum physics, when finding the solution for a radial equation for a hydrogen atom, you need to keep the function of r finite as r approaches infinity to prevent the solution from becoming unphysical. You can accomplish this by putting constraints on the allowable values of the energy, and causing the solution for the radial equation to go to zero as r goes to infinity.
The problem of having
go to infinity as r goes to infinity lies in the form you assume for f(r), which is
The solution is to say that this power series must terminate at a certain index, which you call N. N is called the radial quantum number. So this equation becomes the following (note that the summation is now to N, not infinity):
For this series to terminate, aN+1, aN+2, aN+3, and so on must all be zero. The recurrence relation for the coefficients ak is
For aN+1 to be zero, the factor multiplying ak–1 must be zero for k = N + 1, which means that
Substituting in k = N + 1 gives you
And dividing by 2 gives you
Making the substitution
where n is called the principal quantum number, gives you
This is the quantization condition that must be met if the series for f(r) is to be finite, which it must be, physically:
Because
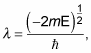
the equation
puts constraints on the allowable values of the energy.

