In quantum physics, you can find the wave function of the ground state of a quantum oscillator, such as the one shown in the figure, which takes the shape of a gaussian curve.
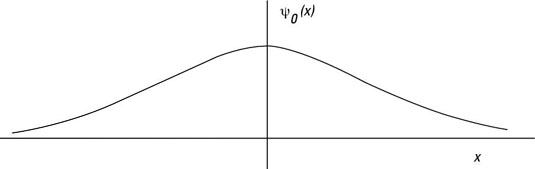
As a gaussian curve, the ground state of a quantum oscillator is
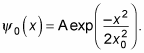
How can you figure out A? Wave functions must be normalized, so the following has to be true:
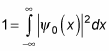
Substituting for
gives you this next equation:
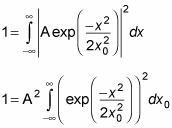
You can evaluate this integral to be
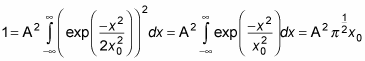
Therefore,
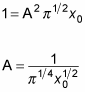
This means that the wave function for the ground state of a quantum mechanical harmonic oscillator is
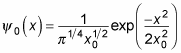
Cool. Now you’ve got an exact wave function.






