In quantum physics, the measure of how different it is to apply operator A and then B, versus B and then A, is called the operators’ commutator. Here’s how you define the commutator of operators A and B:
Two operators commute with each other if their commutator is equal to zero. That is, it doesn’t make any difference in what order you apply them:
Note in particular that any operator commutes with itself:
And it’s easy to show that the commutator of A, B is the negative of the commutator of B, A:
It’s also true that commutators are linear— that is,
And the Hermitian adjoint of a commutator works this way:
You can also find the anticommutator, {A, B}:
Here’s another one: What can you say about the Hermitian adjoint of the commutator of two Hermitian operators? Here’s the answer. First, write the adjoint:
The definition of commutators tells you the following:
In accordance with the properties of adjoints,
Therefore,
But for Hermitian operators,
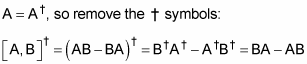
But BA – AB is just
so you have the following:
A and B here are Hermitian operators. When you take the Hermitian adjoint of an expression and get the same thing back with a negative sign in front of it, the expression is called anti-Hermitian, so the commutator of two Hermitian operators is anti-Hermitian. (And by the way, the expectation value of an anti-Hermitian operator is guaranteed to be purely imaginary.)





