You can create the actual eigenstates, | l, m >, of angular momentum states in quantum mechanics. When you have the eigenstates, you also have the eigenvalues, and when you have the eigenvalues, you can solve the Hamiltonian and get the allowed energy levels of an object with angular momentum.
Don't make the assumption that the eigenstates are | l, m >; rather, say they're
where the eigenvalue of
So the eigenvalue of
Similarly, the eigenvalue of
To proceed further, you have to introduce raising and lowering operators. That way, you can solve for the ground state by, for example, applying the lowering operator to the ground state and setting the result equal to zero — and then solving for the ground state itself.
In this case, the raising operator is L+ and the lowering operator is L–. These operators raise and lower the Lz quantum number. You can define the raising and lowering operators this way:
Raising: L+ = Lx + iLy
Lowering: L– = Lx – iLy
These two equations mean that
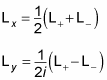
You can also see that
That means the following are all equal to L2:
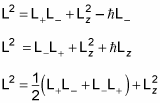
You can also see that these equations are true:
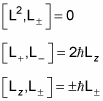
Okay, now you can put all this to work. You're getting to the good stuff.
Take a look at the operation of
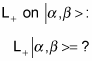
To see what
is, start by applying the Lz operator on it like this:
From
you can see that
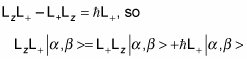
And because
you have the following:
This equation means that the eigenstate
is also an eigenstate of the Lz operator, with an eigenvalue of
Or in a more comprehensible way:
where c is a constant.
So the L+ operator has the effect of raising the
quantum number by 1. Similarly, the lowering operator does this:
Now take a look at what
equals:
Because L2 is a scalar, it commutes with everything. L2 L+ – L+ L2 = 0, so this is true:
And because
you have the following equation:
Similarly, the lowering operator, L–, gives you this:
So the results of these equations mean that the
operators don't change the
at all.





