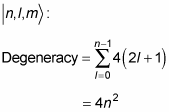How to Calculate the Spin of an Electron in a Hydrogen Atom

When calculating the spin of an electron in a hydrogen atom, you need to allow for the spin of the electron, which provides additional quantum states. Given the following equation, where the wave function of the hydrogen atom is a product of radial and angular parts,

you can add a spin part, corresponding to the spin of the electron, where s is the spin of the electron and m_s is the z component of the spin:

The spin part of the equation can take the following values:

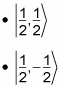
Hence,

now becomes

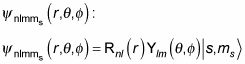
And this wave function can take two different forms, depending on m_s, like this:

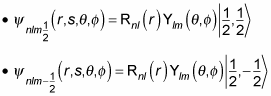
In fact, you can use the spin notation, where

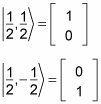
For example, for

you can write the wave function as

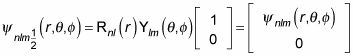
And for

you can write the wave function as

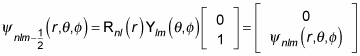
What does this do to the energy degeneracy? If you include the spin of the electron, there are two spin states for every state

so the degeneracy becomes

So if you include the electron’s spin, the energy degeneracy of the hydrogen atom is 2n².

In fact, you can even add the spin of the proton to the wave function (although people don’t usually do that, because the proton’s spin interacts only weakly with magnetic fields applied to the hydrogen atom). In that case, you have a wave function that looks like the following:

where s_e is the spin of the electron, m_se is the z component of the electron’s spin, s_p is the spin of the proton, and m_sp is the z component of the proton’s spin.

If you include the proton’s spin, the wave function can now take four different forms, depending on m_s, like this:

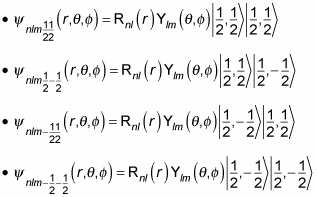
The degeneracy must now include the proton’s spin, so that’s a factor of four for each