If your quantum physics instructor asks you to create symmetric and antisymmetric wave functions for a two-particle system, you can start with the single-particle wave functions:
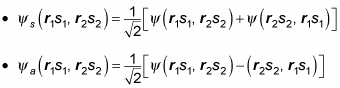
By analogy, here’s the symmetric wave function, made up of two single-particle wave functions:
And here’s the antisymmetric wave function, made up of the two single-particle wave functions:
where ni stands for all the quantum numbers of the ith particle.
Note in particular that
when n1 = n2; in other words, the antisymmetric wave function vanishes when the two particles have the same set of quantum numbers — that is, when they’re in the same quantum state. That idea has important physical ramifications.
You can also write
like this, where P is the permutation operator, which takes the permutation of its argument:
And also note that you can write
like this:
where the term (–1)P is 1 for even permutations (where you exchange both r1s1 and r2s2 and also n1 and n2) and –1 for odd permutations (where you exchange r1s1 and r2s2 but not n1 and n2; or you exchange n1 and n2 but not r1s1 and r2s2).
In fact, people sometimes write
in determinant form like this:
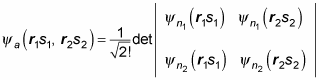
Note that this determinant is zero if n1 = n2.






