In physics, just as you can use formulas to calculate linear velocity, acceleration, displacement, and motion, you can also use equivalent formulas for angular (rotational) movement.
You can think of the angle, theta, in rotational motion just as you think of the displacement, s, in linear motion. This is great, because it means you have an angular counterpart for many of the linear motion equations. Here are the variable substitutions you make to get the angular motion formulas:
Displacement. Instead of s, which you use in linear travel, use
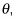
the angular displacement;
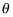
is measured in radians.
Velocity. In place of the velocity, v, use the angular velocity,
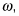
angular velocity is the number of radians covered per second.
Acceleration. Instead of acceleration, a, use the angular acceleration,

the unit for angular acceleration is radians per second2.
The table compares the formulas for both linear and angular motion.

Say, for example, that you have a ball tied to a string. What’s the angular velocity of the ball if you whirl it around? It makes a complete circle,
in 0.5 seconds, so its angular velocity is
Another demonstration of the usefulness of radians in measuring angles is that the linear speed can easily be related to the angular speed. If you take the equation
And multiply both sides by the radius, r, you get
The term
is simply the distance traveled by an object moving in a circle of radius r, so this equation becomes
You may recognize the right side of this equation as the equation for speed. So you can see that linear speed and angular speed are related by
2 seconds, what would its average angular acceleration be? Work it out by plugging in the numbers:





