When you want to find percentiles for a t-distribution, you can use the t-table. A percentile is a number on a statistical distribution whose less-than probability is the given percentage; for example, the 95th percentile of the t-distribution with n – 1 degrees of freedom is that value of
whose left-tail (less-than) probability is 0.95 (and whose right-tail probability is 0.05).
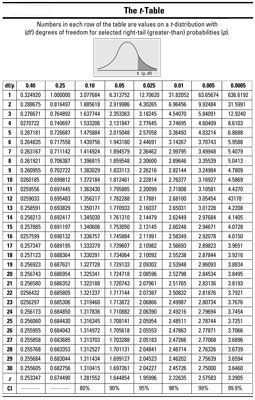
The t-table shows right-tail probabilities for selected t-distributions. You can use it to solve the following problems.
Suppose you have a sample of size 10 and you want to find the 95th percentile of its corresponding t-distribution. You have n – 1= 9 degrees of freedom, so, using the t-table, you look at the row for df = 9. The 95th percentile is the number where 95% of the values lie below it and 5% lie above it, so you want the right-tail area to be 0.05. Move across the row, find the column for 0.05, and you get
This is the 95th percentile of the t-distribution with 9 degrees of freedom.
Now, if you increase the sample size to n = 20, the value of the 95th percentile decreases; look at the row for 20 – 1 = 19 degrees of freedom, and in the column for 0.05 (a right-tail probability of 0.05) you find
degrees of freedom indicate a smaller standard deviation and thus, the t-values are more concentrated about the mean, so you reach the 95th percentile with a value of t closer to 0.





