How to Compare Two Population Proportions

In order to make this comparison, two independent (separate) random samples need to be selected, one from each population. The null hypothesis H₀ is that the two population proportions are the same; in other words, that their difference is equal to 0. The notation for the null hypothesis is H₀: p₁ = p₂, where p₁ is the proportion from the first population, and p₂ is the proportion from the second population.

Stating in H₀ that the two proportions are equal is the same as saying their difference is zero. If you start with the equation p₁ = p₂ and subtract p₂ from each side, you get p₁ – p₂ = 0. So you can write the null hypothesis either way.

where

is the proportion in the first sample with the characteristic of interest,

is the proportion in the second sample with the characteristic of interest,

is the proportion in the combined sample (all the individuals in the first and second samples together) with the characteristic of interest, and z is a value on the Z-distribution. To calculate the test statistic, do the following:

1. Calculate the sample proportions

   

   for each sample. To do this let n₁ and n₂ represent the two sample sizes (they don’t need to be equal). For rho_1, divide the number of individuals in the first sample who have the characteristic of interest by n₁. For rho_2, divide the number of individuals in the second sample who have the characteristic of interest by n₂.

2. Find the difference between the two sample proportions,

   

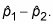
3. Calculate the overall sample proportion

   

   the total number of individuals from both samples who have the characteristic of interest (for example, the total number of smokers, male or female, combined from both samples), divided by the total number of individuals from both samples (n₁ + n₂).

4. Calculate the standard error:

   

5. Divide your result from Step 2 by your result from Step 4.

   This answer is your test statistic.

For example, the makers of Adderall, a drug for attention deficit hyperactivity disorder (ADHD), reported that 26 of the 374 subjects (7 percent) who took the drug experienced vomiting as a side effect, compared to 8 of the 210 subjects (4 percent) who were on a placebo (fake drug). Note that patients didn’t know which treatment they were given.

In the above study, a larger percentage of the people on the drug experienced vomiting, but is this percentage enough to say that the entire population on the drug would experience more vomiting? You can test it to see.

In this example, you have H₀: p₁ – p₂ = 0 versus H_a: p₁ – p₂ > 0, where p₁ represents the proportion of all patients who would vomit when using Adderall, and p₂ represents the proportion of all patients who would vomit when using the placebo.

Why does H_a contain a “>” sign and not a “<” sign? H_a represents the scenario in which those taking Adderall experience more vomiting than those on the placebo — that’s something the FDA (and any candidate for the drug) would want to know about.

But the order of the groups is important, too. You want to set it up so the Adderall group is first, so that when you take the Adderall proportion minus the placebo proportion, you get a positive number if H_a is true. If you switch the groups, the sign would have been negative.

1. First, determine that

   

   Note the sample sizes are n₁ = 374 and n₂ = 210, respectively.

2. Take the difference between these sample proportions to get

   

3. Calculate the overall sample proportion to get

   

4. The standard error is

   

5. Finally, the test statistic is

   

   Whew!

You might ask, “Hey, the difference in the sample proportions is 0.032 which shows that the drug induces more vomiting than the placebo. Why did the hypothesis test reject H₀ since 0.032 is obviously greater than 0?” In this case, 0.032 is not significantly greater than 0. You also need to factor in variation using the standard error and the normal distribution to be able to say something about the entire population of patients.