Exponential functions follow all the rules of functions. However, because they also make up their own unique family, they have their own subset of rules. The following list outlines some basic rules that apply to exponential functions:
The parent exponential function f(x) = bx always has a horizontal asymptote at y = 0, except when b = 1. You can’t raise a positive number to any power and get 0 or a negative number.
The domain of any exponential function is

This rule is true because you can raise a positive number to any power. However, the range of exponential functions reflects that all exponential functions have horizontal asymptotes. All parent exponential functions (except when b = 1) have ranges greater than 0, or

The order of operations still governs how you act on the function. When the idea of a vertical transformation applies to an exponential function, most people take the order of operations and throw it out the window. Avoid this mistake. For example,

You can’t multiply before you deal with the exponent.
You can’t have a base that’s negative. For example, y = (–2)x isn’t an equation you have to worry about graphing in pre-calculus. If you’re asked to graph y = –2x, don’t fret. You read this as “the opposite of 2 to the x,” which means that (remember the order of operations) you raise 2 to the power first and then multiply by –1. This simple change flips the graph upside down and changes its range to

A number with a negative exponent is the reciprocal of the number to the corresponding positive exponent. For instance, y = 2–3 doesn’t equal (–2)3 or –23. Raising any number to a negative power takes the reciprocal of the number to the positive power:

When you multiply monomials with exponents, you add the exponents. For instance,

If you break down the problem, the function is easier to see:

When you have multiple factors inside parentheses raised to a power, you raise every single term to that power. For instance, (4x3y5)2 isn’t 4x3y10; it’s 16x6y10.
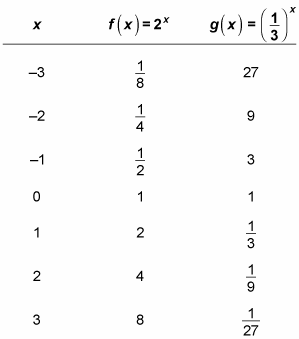
When graphing an exponential function, remember that the graph of an exponential function whose base number is greater than 1 always increases (or rises) as it moves to the right; as the graph moves to the left, it always approaches 0 but never actually get there. For example, f(x) = 2x is an exponential function, as is

The table shows the x and y values of these exponential functions. These parent functions illustrate that, as long as the exponent is positive, the graph of an exponential function whose base is greater than 1 increases as x increases — an example of exponential growth — whereas the graph of an exponential function whose base is between 0 and 1 decreases towards the x-axis as x increases — an example of exponential decay.
The graph of an exponential function who base numbers is fractions between 0 and 1 always rise to the left and approach 0 to the right. This rule holds true until you start to transform the parent graphs.