The Differences between Pre-Calculus and Calculus

Every good thing must come to an end, and for pre-calculus, the end is actually the beginning — the beginning of calculus. Calculus includes the study of change and rates of change (not to mention a big change for you!). Before calculus, everything was usually static (stationary or motionless), but calculus shows you that things can be different over time. This branch of mathematics enables you to study how things move, grow, travel, expand, and shrink and helps you do so much more than any other math subject before.

Here are a few basic distinctions between pre-calculus and calculus to illustrate the change in subject:

• Pre-calculus: You study the slope of a line.

Calculus: You study the slope of a tangent line to a point on a curve.

A straight line has the same slope all the time. No matter which point you choose to look at, the slope is the same. However, because a curve moves and changes, the slope of the tangent line is different at different points on the curve.

• Pre-calculus: You study the area of geometric shapes.

Calculus: You study the area under a curve.

In pre-calculus, you can rest easy knowing that a geometric shape is always basically the same, so you can find its area with a formula using certain measurements and a standard formula. A curve goes on forever, and depending on which section you’re looking at, its area changes. No more nice, pretty formulas to find area here; instead, you use a process called integration (which can also be termed nice and pretty).

• Pre-calculus: You study the volume of a geometric solid.

Calculus: You study the volume of interesting shapes called solids of revolution.

The geometric solids you find volume for (prisms, cylinders, and pyramids, for example) have formulas that are always the same, based on the basic shapes of the solids and their dimensions. The way to find the volume of a solid of revolution, though, is to cut the shape into infinitely small slices and find the volume of each slice. The volume of the slices changes over time based on the section of the curve you’re looking at.

• Pre-calculus: You study objects moving with constant velocities.

Calculus: You study objects moving with acceleration.

Using algebra, you can find the average rate of change of an object over a certain time interval. Using calculus, you can find the instantaneous rate of change for an object at an exact moment in time.

• Pre-calculus: You study functions in terms of

Calculus: You study changes to functions in terms of x, with those changes in terms of t.

Graphs of functions referred to as f(x), can be created by plotting points. In calculus, you describe the changes to the graph f(x) by using the variable t, indicated by

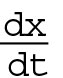
Calculus is best taken with an open mind and the spirit of adventure! Don’t view calculus as a new bunch of material to memorize. Instead, try to build on your pre-calculus knowledge and experience. Try to glean an understanding of why calculus does what it does. In this arena, concepts are key.