When you apply a vertical transformation to a parent graph, you are stretching or shrinking the graph along the y-axis, which changes its height. A number (or coefficient) multiplying in front of a function causes the vertical transformation. The coefficient always affects the height of each and every point in the graph of the function. We call the vertical transformation a stretch if the coefficient is greater than 1 and a shrink if the coefficient is between 0 and 1.
For example, the graph of f(x) = 2x2 takes the graph of f(x) = x2 and stretches it by a vertical factor of two. That means that each time you plot a point vertically on the graph, the value gets multiplied by two (making the graph twice as tall at each point). For example, in f(x)=x2, 1 gets mapped to 2×12=2, 2 gets mapped to 2×22=8, 3 gets mapped to 2×32=18, etc.
The vertical transformation of f(x) = 2x2 and
are shown in this figure.
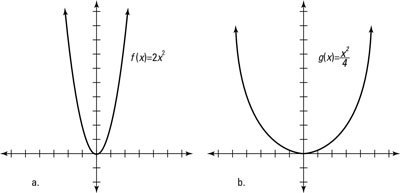
The transformation rules apply to any function, so the vertical transformation of
is shown here.
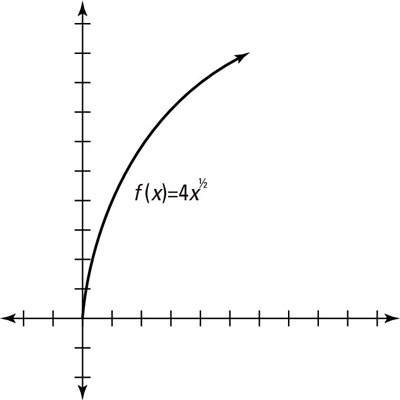
The 4 is a vertical stretch; it makes the graph four times as tall at every point. For example, 1 gets mapped to 4×sqrt(1)=4, 4 gets mapped to 4×sqrt(4)=8, 9 gets mapped to 4×sqrt(9)=12, etc. (notice that this example uses numbers that you can easily take the square root of to make graphing a simple task); and so on.





