When you apply a horizontal transformation to a parent graph, you are stretching or shrinking the graph horizontally, along the x-axis. A number multiplying a variable inside a function affects the horizontal position of the graph — a little like the fast-forward or slow-motion button on a remote control, making the graph move faster or slower. A coefficient greater than 1 causes the function to shrink horizontally, making it appear to move faster. A coefficient between 0 and 1 makes the function appear to move slower, or a horizontal stretch.
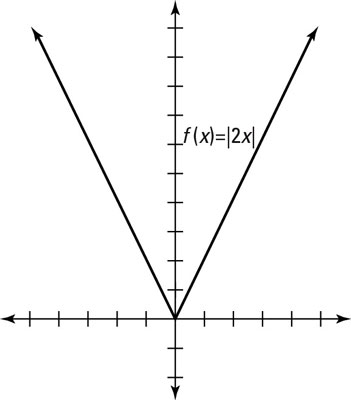
For instance, look at the graph of f(x) = |2x| in the preceding figure. If the distance between any two x values in the parent graph is 1, then those x-values will correspond (based on the values they get mapped to) to x-values for the graph f(x)=|2x| having a distance of ½. To see this, set the inside of the new, transformed function equal to the distance between the x values, you get 2x = 1. Solving the equation gives you x = 1/2 Hence in the parent graph we have the points (0,0) , (1,1), (2,2), (3,3), etc.; yet in f(x)=|2x| we have the points (0,0) , (1/2,1), (1,2),(3/2.3), etc.





