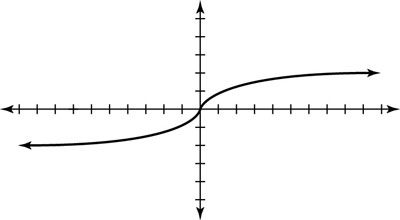
In mathematics, you see certain graphs over and over again. For that reason, these original, common functions are called parent graphs, and they include graphs of quadratic functions, square roots, absolute values, cubics, and cube roots.
Graphing quadratic functions
Quadratic functions are functions in which the 2nd power, or square, is the highest to which the unknown quantity or variable is raised.. The function y=x2or f(x) = x2 is a quadratic function, and is the parent graph for all other quadratic functions.
The shortcut to graphing the function f(x) = x2 is to start at the point (0, 0) (the origin) and mark the point, called the vertex. Note that the point (0, 0) is the vertex of the parent function only. In calculus, this point is called a critical point, and some pre-calculus teachers also use that terminology. Without getting into the calculus definition, it means that the point is special.
The graph of any quadratic function is called a parabola. All parabolas have the same basic shape. To get the other points, you plot the points (1,12)=(1,1), (2,22)=(2,4), (3,32)=(3,9), etc. This graphing occurs on the other side of the vertex as well and keeps going, but usually just a couple points on either side of the vertex gives you a good idea of what the graph looks like.
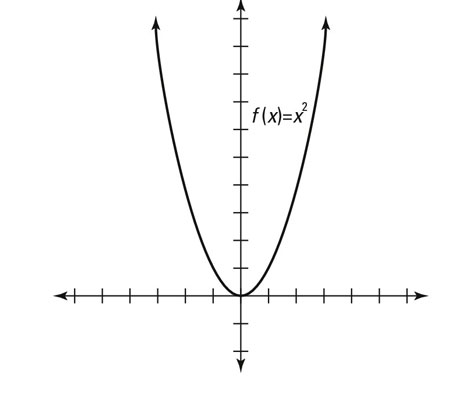
This figure shows an example of a quadratic function in graph form.
Graphing square-root functions
A square-root graph is related to a quadratic graph. The quadratic graph is f(x) = x2, whereas the square-root graph is g(x) = x1/2. The graph of a square-root function looks like the left half of a parabola that has been rotated 90 degrees clockwise. You can also write the square-root function as
However, only half of the parabola exists, for two reasons. First, its parent graph exists only when x is zero or positive (because you can’t find the square root of negative numbers [and keep them real, anyway]). Secondly, the parabola exists only when g(x) is positive because when you are asked to find
you’re being asked to find only the principal or positive root of x..
This graph starts at the origin (0, 0) and then moves to (1, sqrt(1))=(1,1), (2, sqrt(2)) , (3, sqrt(3)), etc.
This figure,
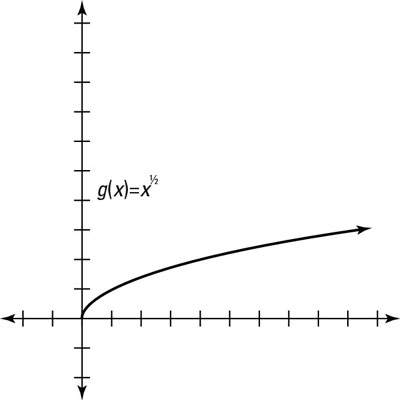
shows the graph for the parent square-root function
Notice that the values you get by plotting consecutive points don’t exactly give you the nicest numbers. Instead, try picking values for which you can easily find the square root. Here’s how this works: Start at (0,sqrt(0))=(0,0), then go to (1,sqrt(1))=(1,1), then to (4,sqrt(4))=(4,2), then to (9,sqrt(9))=(9,3), etc.
Graphing absolute-value functions
The absolute-value parent graph of the function y = |x| turns all inputs non-negative (0 or positive). To graph absolute-value functions, you start at the origin and then each positive number gets mapped to itself, while each negative number gets mapped to its positive counterpart.
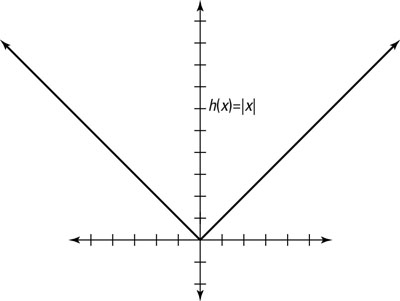
This figure shows the graph of an absolute-value function.
Graphing cubic functions
In a cubic function, the highest degree on any variable is three. The function f(x) = x3 is the parent function. You start graphing the cubic function parent graph at the origin (0, 0).
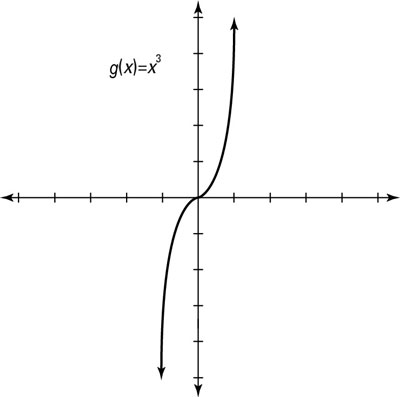
From (0,0), you graph (1,13)=(1,1), (2,23)=(2,8), etc. to the left of (0,0) you graph (-1,(-1)3)=(-1,-1), (-2,(-2)3)=(-2,-8), etc.. The cubic parent function, g(x) = x3, is shown in graph form in this figure.
Graphing cube-root functions
Cube-root functions are related to cubic functions in the same way that square-root functions are related to quadratic functions. You write cubic functions as f(x) = x3 and cube-root functions as g(x) = x1/3 or
Noting that a cube-root function is odd is important because it helps you graph it.