An ellipse is basically a circle that has been squished either horizontally or vertically. From a pre-calculus perspective, an ellipse is a set of points on a plane, creating an oval, curved shape such that the sum of the distances from any point on the curve to two fixed points (the foci) is a constant (always the same).
Graphically speaking, you must know two different types of ellipses: horizontal and vertical. A horizontal ellipse is short and fat; a vertical one is tall and skinny. Each type of ellipse has these main parts:
Center. The point in the middle of the ellipse is called the center and is named (h, v) just like the vertex of a parabola and the center of a circle.
Major axis. The major axis is the line that runs through the center of the ellipse the long way. The variable a is the letter used to name the distance from the center to the ellipse on the major axis. The endpoints of the major axis are on the ellipse and are called vertices.
Minor axis. The minor axis is perpendicular to the major axis and runs through the center the short way. The variable b is the letter used to name the distance to the ellipse from the center on the minor axis. Because the major axis is always longer than the minor one, a > b. The endpoints on the minor axis are called co-vertices.
Foci. The foci are the two points that dictate how fat or how skinny the ellipse is. They are always located on the major axis, and can be found by the following equation: a2 – b2 = F2 where a and b are mentioned as in the preceding bullets and F is the distance from the center to each focus.
 The labels of a horizontal ellipse and a vertical ellipse.
The labels of a horizontal ellipse and a vertical ellipse.
Figure a shows a horizontal ellipse with its parts labeled; Figure b shows a vertical one. Notice that the length of the major axis is 2a and the length of the minor axis is 2b. This figure also shows the correct placement of the foci — always on the major axis.
Two types of equations apply to ellipses, depending on whether they're horizontal or vertical. The horizontal equation has the center at (h, v), major axis of 2a, and minor axis of 2b:
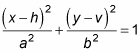
The vertical equation has the same parts, although a and b switch places:
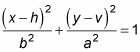
Note that when the bigger number a is under x, the ellipse is horizontal; when the bigger number is under y, it's vertical.





