The properties of the parallelogram are simply those things that are true about it. These properties concern its sides, angles, and diagonals.
The parallelogram has the following properties:
Opposite sides are parallel by definition.
Opposite sides are congruent.
Opposite angles are congruent.
Consecutive angles are supplementary.
The diagonals bisect each other.
If you just look at a parallelogram, the things that look true (namely, the things on this list) are true and are thus properties, and the things that don’t look like they’re true aren’t properties.
If you draw a picture to help you figure out a quadrilateral’s properties, make your sketch as general as possible. For instance, as you sketch your parallelogram, make sure it’s not almost a rhombus (with four sides that are almost congruent) or almost a rectangle (with four angles close to right angles). If your parallelogram sketch is close to, say, a rectangle, something that’s true for rectangles but not true for all parallelograms (such as congruent diagonals) may look true and thus cause you to mistakenly conclude that it’s a property of parallelograms. Capiche?
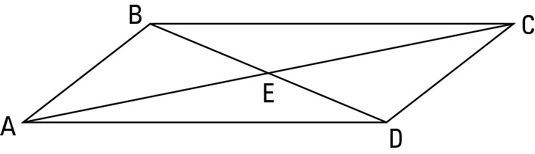
Imagine that you can’t remember the properties of a parallelogram. You could just sketch one (as in the above figure) and run through all things that might be properties. (Note that this parallelogram does not come close to resembling a rectangle of a rhombus.)
The following questions concern the sides of a parallelogram (refer to the preceding figure).
Do the sides appear to be congruent?
Yes, opposite sides look congruent, and that’s a property. But adjacent sides don’t look congruent, and that’s not a property.
Do the sides appear to be parallel?
Yes, opposite sides look parallel (and of course, you know this property if you know the definition of a parallelogram).
The following questions explore the angles of a parallelogram (refer to the figure again).
Do any angles appear to be congruent?
Yes, opposite angles look congruent, and that’s a property. (Angles A and C appear to be about 45°, and angles B and D look like about 135°).
Do any angles appear to be supplementary?
Yes, consecutive angles (like angles A and B) look like they’re supplementary, and that’s a property. (Using parallel lines

angles A and B are same-side interior angles and are therefore supplementary.)
Do any angles appear to be right angles?
Obviously not, and that’s not a property.
The following questions address statements about the diagonals of a parallelogram
Do the diagonals appear to be congruent?
Not even close (in the above figure, one is roughly twice as long as the other, which surprises most people) — not a property.
Do the diagonals appear to be perpendicular?
Not even close; not a property.
Do the diagonals appear to be bisecting each other?
Yes, each one seems to cut the other in half, and that’s a property.
Do the diagonals appear to be bisecting the angles whose vertices they meet?
No.

Not a property.





