You can solve some circle problems using the Tangent-Secant Power Theorem. This theorem states that if a tangent and a secant are drawn from an external point to a circle, then the square of the measure of the tangent is equal to the product of the measures of the secant’s external part and the entire secant. (Sounds sort of like the scarecrow from the Wizard of Oz talking about the Pythagorean Theorem. Remember that?)
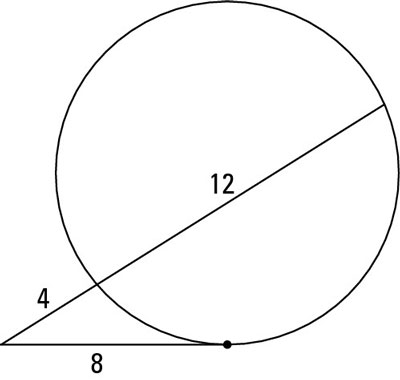
For example, in the above figure,
Here’s a nifty application of the Tangent-Secant Power Theorem. Check out the following figure of an adult of average height (say 5'7" or 5'8") standing at the ocean’s shore.
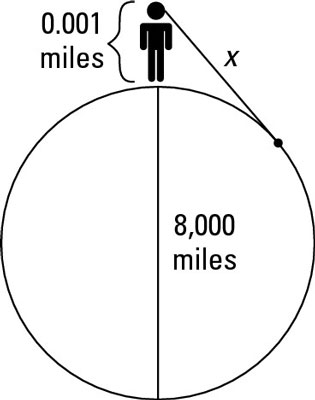
The eyes of someone of average height are about 5.3 feet above the ground, which is very close to 1/1,000 mile. The Earth’s diameter is about 8,000 miles. And x in the figure represents the distance to the horizon. You can plug everything into the Tangent-Secant Power Theorem and solve for x:

This short distance surprises most people. If you’re standing on the shore, something floating on the water begins to drop below the horizon at a mere 2.8 miles from shore!





