The ratio test looks at the ratio of a general term of a series to the immediately preceding term. The ratio test works by looking only at the nature of the series you’re trying to figure out (as opposed to the tests which compare the test you’re investigating to a known, benchmark series). If, in the limit, this ratio is less than 1, the series converges; if it’s more than 1 (this includes infinity), the series diverges; and if it equals 1, you learn nothing, and must try a different test.
The ratio test works especially well with series involving factorials such as n! or where n is in the power, like
Keep in mind that the factorial symbol (!) tells you to multiply like this: 6! = 6 · 5 · 4 · 3 · 2 · 1. And notice how things cancel when you have factorials in the numerator and denominator of a fraction:

In both cases, everything cancels but the 6. In the same way
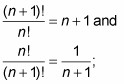
everything cancels but the (n + 1). Last, it seems weird, but 0! = 1.
Try this one: Does
converge or diverge? Here’s what you do. You look at the limit of the ratio of the (n + 1)st term to the nth term:

Here’s another series:
What’s your guess — does it converge or diverge? Look at the limit of the ratio:






