In geometry, you learned how to figure the volumes of simple solids like boxes, cylinders, and spheres. Integration enables you to calculate the volumes of an endless variety of much more complicated shapes.
The meat-slicer metaphor is actually quite accurate. Picture a hunk of meat being cut into very thin slices on one of those deli meat slicers. That’s the basic idea here. You slice up a three-dimensional shape, then add up the volumes of the slices to determine the total volume.
Here’s a problem: What’s the volume of the solid whose length runs along the x-axis from 0 to ð and whose cross sections perpendicular to the x-axis are equilateral triangles such that the midpoints of their bases lie on the x-axis and their top vertices are on the curve y = sin(x)? Is that a mouthful or what? This problem is almost harder to describe and to picture than it is to do. Take a look at this thing in the following figure.
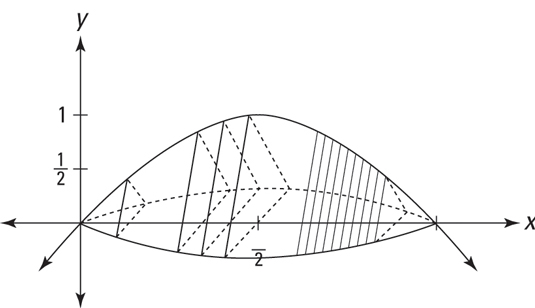
So what’s the volume?
Determine the area of any old cross section.
Each cross section is an equilateral triangle with a height of sin(x).

Find the volume of a representative slice.
The volume of a slice is just its cross-sectional area times its infinitesimal thickness, dx. So you’ve got the volume:

Add up the volumes of the slices from 0 to pi by integrating.
If the following seems a bit difficult, well, heck, you better get used to it. This is calculus after all. (Actually, it’s not really that bad if you go through it patiently, step by step.)

It’s a piece o’ cake slice o’ meat.





