You can use calculus to determine a rate that’s related to the speed of a moving object. For example, say a pitcher delivers a fastball, which the batter pops up — it goes straight up above home plate. When it reaches a height of 60 feet, it’s moving up at a rate of 50 feet per second. At this point, how fast is the distance from the ball to second base growing? Note: The distance between the bases of a baseball diamond is 90 feet.

Draw your diagram and label it as shown in the figure.
List all given rates and the rate you’re asked to figure out.

Write a formula that involves the variables:

The Pythagorean Theorem is frequently used in related rate problems that involve a right triangle.
Differentiate with respect to time:

Substitute known values into this equation and solve for dd/dt:
You’re missing a needed value, d. So use the Pythagorean Theorem again to get it:
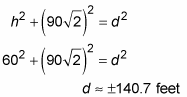
(You can reject the negative answer.) Now do the substitutions:

So the distance is growing at a rate of approximately 21.3 feet/second.






