The difference quotient should have a cape and boots because it has such a useful super-power: it gives you the slope of a curve at a single point. Want to know how?
First, look at this figure.
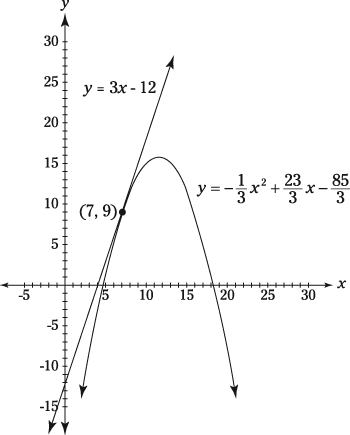
You can see that the slope of the parabola at (7, 9) equals 3, the slope of the tangent line. But you can't calculate that slope with the algebra slope formula
because no matter what other point on the parabola you use with (7, 0) to plug into the formula, you'll get a slope that's steeper or less steep than the precise slope of 3 at (7, 9).
Now, what if your second point on the parabola were extremely close to (7, 9) — for example,
In this case, your line would be almost exactly as steep as the tangent line. The difference quotient gives the precise slope of the tangent line by sliding the second point closer and closer to (7, 9) until its distance from (7, 9) is infinitely small.
Okay, enough of this mumbo jumbo; now for the math. Here's the definition of the derivative based on the difference quotient:
Note that, as with most limit problems, plugging the arrow-number in at the beginning of a difference quotient problem won't help because that gives you
As you'll see in the following practice questions, you have to do a little algebraic mojo so that you can cancel the h and then plug in.
Practice questions
Use the difference quotient to determine the derivative of the line y = 4x – 3.
Use the difference quotient to find the derivative of the parabola f (x) = 3x2.
Answers and explanations
The derivative is
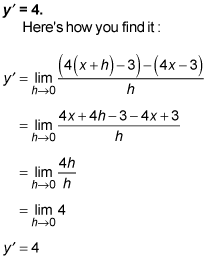
Of course, you can also figure this out because the slope of y = 4x – 3 is 4.
The derivative is


