The product rule and the quotient rule are a dynamic duo of differentiation problems. They're very useful because the product rule gives you the derivatives for the product of two functions, and the quotient rule does the same for the quotient of two functions.
Before you tackle some practice problems using these rules, here's a quick overview of how they work.
The product rule is a snap. The derivative of a product of two functions,
The quotient rule is also a piece of cake. The derivative of a quotient of two functions,
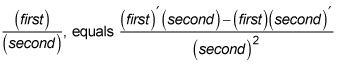
Here's a good way to remember the quotient rule. When you read a product, you read from left to right, and when you read a quotient, you read from top to bottom. So just remember that the quotient rule, like the product rule, works in the natural order in which you read, beginning with the derivative of the first thing you read. For some mysterious reason, many textbooks give the quotient rule in a different form that's harder to remember. Learn it the way it's written here, beginning with
That's the easiest way to remember it. Also note that when the two rules are written as they are here, the numerator of the quotient rule looks exactly like the product rule, except that there's a minus sign instead of a plus sign.
Now, onto the practice questions.
Practice questions
Find the derivative using the product rule:

Find the derivative using the quotient rule:

Answers and explanations
Using the product rule, the derivative is

How do you find this? First, remember that

Using the quotient rule, the derivative is






