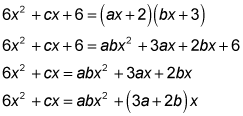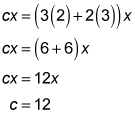The following practice questions may look scary, but they simply involve a little distribution, simplifying, and plugging in of values.
Practice questions
- Given this equation, what is the value of a + b + c? x(2x + 3) – 2(x – 3) = ax2 + bx + c
- If a, b, and c are integers, 6x2 + cx + 6 = (ax + 2)(bx + 3) for all values of x, and 1 < a < b, what is the value of c?
Answers and explanations
- The correct answer is 9.
Distribute and simplify the expressions on the left to match the quadratic on the right:
From this, you know that a = 2, b = 1, and c = 6, which add up to 9.
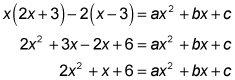
- The correct answer is 12.
Multiply the binomials to match the quadratic, and then simplify by subtracting 6 from both sides:
Because 6x2 = abx2, ab = 6. And because a and b are integers and 1 < a < b, you know that a = 2 and b = 3. Now, using cx = (3a + 2b)x, you can plug in 2 for a and 3 for b and then solve for c: