The Praxis Core algebra test will expect you to be familiar with systems of equations. Equations with two variables can be solved if they are accompanied by a second equation with at least one of the variables.
When presented with such sets of equations, or systems of equations, the trick is to use the information to get an equation with one variable. Two major methods exist for accomplishing this: the substitution method and the elimination method.
Solving by substitution
The substitution method involves finding the value of one variable in terms of the other in one equation. Then you can substitute that expression for the variable in the second equation. The result is an equation with one variable, and you can solve an equation with one variable by using the earlier discussed techniques.
4x + 2y = 22
x + y = 8
The concept is that x has the same value in both equations and so does y. To solve the system of equations using the substitution method, you state either what y equals in terms of x or what x equals in terms of y. You can use either equation to make the determination, but the second equation is easier to work with because neither variable has a pesky coefficient.
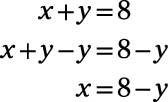
Because x has exactly the same value as 8 – y, you can substitute 8 – y for x in the other equation. Then you have an equation with just one variable.
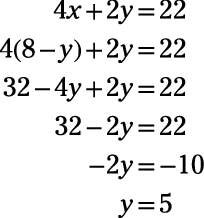
You can solve the equation to determine that y = 5. Then, you can substitute 5 for y in either equation and solve for x, which is 3.
When using the substitution method to solve a system of equations, make sure you don’t substitute a variable expression for the other variable in the equation you used to determine the expression. You must use the other equation; otherwise, the result will be an equation with no variable. An equation with no variable can’t be solved.
Solving by elimination
Another method used for solving systems of equations is elimination. It’s based on the fact that adding the same value to or subtracting the same value from both sides of a true equation results in another true equation. In this case, the added or subtracted value is what is represented by both sides of one of the given equations. Check out this example:
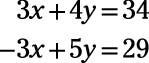
Because both sides of the second equation (and the first, for that matter) have the same value, the second equation can be added to the first equation. The result is a third equation that is also true.
That’s an ideal thing to do here because adding 3x and –3x gets rid of x, leaving you an equation with only one variable, y. The coefficients of x have the same absolute value, so elimination can work immediately. You may sometimes have to subtract.
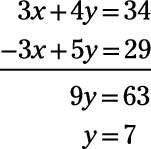
Knowing that y = 7, you can put 7 in for y in either equation to determine that x = 2.
With both elimination and substitution, putting a variable value in place of the variable does not cause trouble. Just don’t substitute an algebraic expression for a variable in the equation that gave you the expression. That’s where chaos awaits.
To use elimination when neither variable has coefficients with the same absolute value, you can multiply both sides of an equation by the same number and get a new equation. In some cases, you must do that to both equations. Consider the following equations:
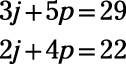
Neither variable has coefficients with the same absolute value, but you can multiply both sides of the top equation by 2 and both sides of the bottom equation by 3 to give j the same coefficient.
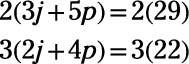
Then you can subtract one equation from the other and get an equation with one variable.
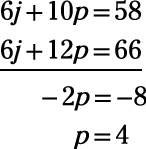
Now that you know p = 4, you can substitute 4 in for p in either equation and solve for j, which has a value of 3.
Substitution is the ideal method to use when at least one of the variable terms has a coefficient of 1 (understood). Elimination is the generally preferred method to use when both variables have coefficients other than 1 in all cases.





