How do you multiply and divide variables for the Praxis Core exam? Just as you can add and subtract terms and expressions, you can multiply and divide them. Remember that variables represent numbers, which means operations with variables involve the same principles that apply to operations without variables. So, when in doubt, just think about how numbers work.
Multiplying expressions
In multiplying algebraic expressions, the number of times a number or variable is a factor is part of what determines what the product is. To multiply different variables, simply put them next to each other.
a × b = ab
To multiply a number times a variable or variables, put them all next to each other.
3 × a × b = 3ab
The next question is what you should do when the same variable is a factor more than once. Do you write the variable next to itself? Nope.
The product has to be written with exponents because a letter times a letter does not equal another letter. The letters have to remain the same, but their exponents do not. The final answer should have exponents representing how many times a variable is a factor.
(x)(x)(x) = x3
j × j = j2
p × p × p × p = p4
Using 1 as an exponent isn’t necessary. A variable without an exponent shown is understood to have an exponent of 1.
Now put these principles together in your mind, and you’re ready to multiply algebraic terms that have coefficients.
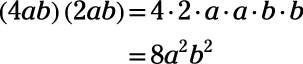
Now, what do you do when the terms you are multiplying already have exponents? For each variable, you just add its exponents.
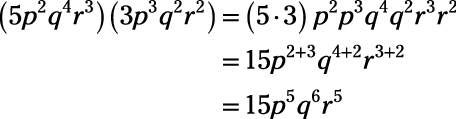
With these skills, you can multiply any algebraic terms. On the Praxis Core, you may be asked to multiply two-term expressions. For example, you may need to multiply (x + 2)(x + 3). To find the product of two two-term expressions, the best method to use is FOIL, which is the best-known algebra acronym. It stands for “first, outer, inner, last.”
The words apply to the terms in the problem. In this case, the first terms are x and x, the outer terms are x and 3, the inner terms are 2 and x, and the last (as in last in each expression) terms are 2 and 3. To use FOIL, multiply the first, outer, inner, and last terms, and then add them together in the same order.
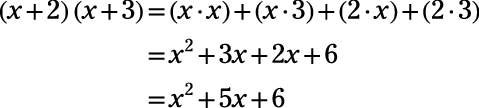
Subtracting a number is the same as adding its opposite. A minus sign in a FOIL problem must be treated as a negative sign.
Find the following product: (3j + 4)(2j – 5)
(A) 5j2 – 7j – 20
(B) 6j2 – 7j – 20
(C) 6j2 + 7j + 20
(D) 13j3 – 1
The correct answer is Choice (B). By using FOIL, you can determine that the product of the two expressions is (3j)(2j) + (3j)(–5) + (4)(2j) + (4)(–5), which is 6j2 – 15j + 8j – 20. By combining those terms, you get 6j2 – 7j – 20.
Dividing expressions
Dividing algebraic terms isn’t as common as multiplying them, but it does happen, so you should know how to perform this operation.
In a fraction, the numerator is divided by the denominator.
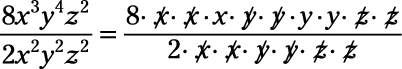
Recall that factors that appear in a term that is a numerator and a term that is the denominator of the same fraction can be cancelled once in both numerator and denominator for every appearance in both. In other words, anything that is a factor of a fraction’s numerator and denominator can be cancelled from both, but it can be cancelled only one time for each instance.
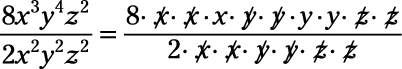
What’s left in the preceding ratio? 8/2 = 4, so 4 is left in the numerator. With 3 x’s on top and 2on the bottom, 1 is left on top because 3 – 2 = 1. By the same reasoning, 2 y’s are left in the numerator. The z’s cancel each other out. Therefore, you’re left with 4xy2.
Because of this principle, you can easily find the difference of a variable’s numerator and denominator exponents. Just subtract the smaller exponent from the bigger exponent and make the difference the variable’s resulting exponent.
Put the variable with that exponent in the place where the bigger exponent was before you subtracted. If a variable in a problem has the same exponent in the numerator and denominator, you can cancel the variable completely. The result of exponent subtraction would be the variable with an exponent of 0, and any value with an exponent of 0 equals 1.
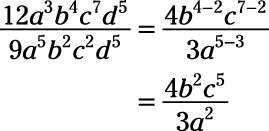
Similarly, when you divide one product of multi-term expressions by another, you can cancel expressions that are factors of both the dividend and the divisor.
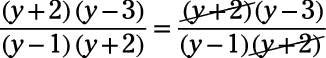
Now you’re left with one expression on top and one on the bottom. The quotient is:
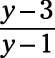
On the Praxis Core exam, you may be asked to divide with expressions that have three or more terms.





