You will need to know how to find factors of whole numbers for the Praxis Core mathematics exam. A factor of a whole number is a whole number that can be divided into it a whole number of times. For example, 4 is a factor of 20 because 4 can be multiplied by the whole number 5 (which is also a factor of 20) to get 20.
The number 4 is not a factor of 21, 19, or any other number that is not evenly divisible by 4. And if you can break down a number’s factor even further into its own factors, those smaller factors are also factors of the original number you started with. For example, because 2 is a factor of 4, 2 is also a factor of 20.
Every whole number has itself and 1 for factors. If those are the only two factors of a number, it’s a prime number. For example, 3, 17, 31, and 79 are prime numbers.
To determine the factors of a number, first determine one factor and what it has to be multiplied by to get the number. Then find factors of those numbers the same way. Continue the process until no numbers can be broken down further.
At this point, you’ve found the prime factorization of the number — a representation of the number as a product of all its prime factors. From there, all the number’s factors, other than 1, can be found by multiplying every possible combination of the prime factors.
Find all the factors of 30.
(A) 30 and 1
(B) 2, 3, and 5
(C) 1, 2, 3, 5, 6, 10, 15, and 30
(D) 2, 3, 5, 6, 10, and 15
(E) 2 and 15
The correct answer is Choice (C). All the numbers listed are either prime factors of 30, products of combinations of those prime factors, or 1. However, Choice (C) is the only choice that includes all of them.
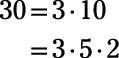
The number 1 is a factor of 30 because 30 is a whole number, and every whole number is a factor of itself. The prime factors of 30 are 5, 2, and 3. By multiplying combinations of those numbers, the other factors can be determined.
5 × 2 = 10; 10 × 3 = 30
5 × 3 = 15; 15 × 2 = 30
2 × 3 = 6; 6 × 5 = 30

