Quadratic equations will likely appear on the ASVAB.A quadratic equation is an algebraic equation in which the unknown is raised to an exponent no higher than 2, as in x2. They can be very simple or very complex (or several degrees of difficulty in between). Here are some examples:
x2 = 36
x2 + 4 = 72
x2 + 3x – 33 = 0
The exponent in quadratics is never higher than 2. An equation that includes the variable x3 or x4 is not a quadratic.
You can solve quadratics in three primary ways: the square-root method, factoring, or the quadratic formula. Which method you choose depends on the difficulty of the equation.
Method 1: The square-root method
Simple quadratic equations (those that consist of just one squared term and a number) can be solved by using the square-root rule:
as long as k isn’t a negative number.
Remember to include the ± sign, which indicates that the answer is a positive or negative number. Take the following simple quadratic equation:
Solve: 3x2 + 4 = 31.
First, isolate the variable by subtracting 4 from each side.
The result is 3x2 = 27.
Next, get rid of the 3 by dividing both sides of the equation by 3.
The result is x2 = 9.
You can now solve by using the square root rule.

Method 2: The factoring method
Most quadratic equations you encounter on the ASVAB math subtests can be solved by putting the equation into the quadratic form and then factoring.
The quadratic form is ax2 + bx + c = 0, where a, b, and c are just numbers. All quadratic equations can be expressed in this form. Want to see some examples?
2x2– 4x= 32: This equation can be expressed in the quadratic form as 2x2 + (–4x) + (–32) = 0. So a = 2, b = –4, and c = –32.
x2= 36: You can express this equation as 1x2 + 0x + (–36) = 0. So a = 1, b = 0, and c = –36.
3x2+ 6x+ 4 = –33: Expressed in quadratic form, this equation reads 3x + 6x + 37 = 0. So a = 3, b = 6, and c = 37.
Ready to factor? How about trying the following equation?
Solve: x2 + 5x + 6 = 0.
This is already expressed in quadratic form, saving you a little time.
You can use the factoring method for most quadratic equations where a = 1 and c is a positive number.
The first step in factoring a quadratic equation is to draw two sets of parentheses on your scratch paper, and then place an x at the front of each, leaving some extra space after it. As with the original quadratic, the equation should equal zero:
(x )(x ) = 0
The next step is to find two numbers that equal c when multiplied together and equal b when added together. In the example, b = 5 and c = 6, so you need to hunt for two numbers that multiply to 6 and add up to 5. For example, 2 × 3 = 6 and 2 + 3 = 5.
In this case, the two numbers you’re seeking are positive 2 and positive 3.
Finally, put these two numbers into your set of parentheses:
(x + 2)(x + 3) = 0
This means that x + 2 = 0, and/or x + 3 = 0. The solution to this quadratic equation is x = –2 and/or x = –3.
When choosing your factors, remember that they can be either positive or negative numbers. You can use clues from the signs of b and c to help you find the numbers (factors) you need:
If c is positive, then the factors you’re looking for are either both positive or both negative:
If b is positive, then the factors are positive.
If b is negative, then the factors are negative.
b is the sum of the two factors that give you c.
If c is negative, then the factors you’re looking for are of alternating signs; that is, one is negative and one is positive:
If b is positive, then the larger factor is positive.
If b is negative, then the larger factor is negative.
b is the difference between the two factors that give you c.
Try another one, just for giggles:
Solve: x2 – 7x + 6 = 0.
Start by writing your parentheses:
(x )(x ) = 0
In this equation, b = –7 and c = +6. Because b is negative and c is positive, both factors will be negative.
You’re looking for two negative numbers that multiply to 6 and add to –7. Those numbers are –1 and –6. Plugging the numbers into your parentheses, you get (x – 1)(x – 6) = 0. So x = 1 and/or x = 6.
Method 3: The quadratic formula
The square-root method can be used for simple quadratics, and the factoring method can easily be used for many other quadratics, as long as a = 1. But what if a doesn’t equal 1, or you can’t easily find two numbers that multiply to c and add up to b?
You can use the quadratic formula to solve any quadratic equation. But, you may not want to because the quadratic formula is kind of complex:
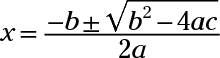
The quadratic formula uses the a, b, and c from ax2 + bx + c = 0, just like the factoring method.
Armed with this knowledge, you can apply your skills to a complex quadratic equation:
Solve: 2x2 – 4x – 3 = 0.
In this equation, a = 2, b = –4, and c = –3. Plug the known values into the quadratic formula:
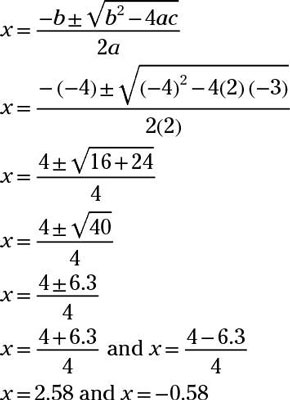
Rounded to the nearest tenth, x = 2.6 and x = –0.6.





