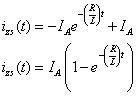
After fiddling with the math, you determine that the zero-input response of the sample circuit is this:
![]()
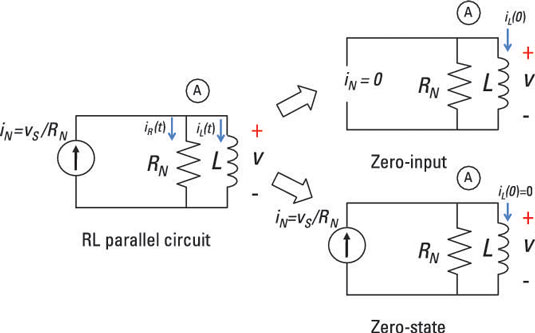
Now you are ready to calculate the zero-state response for the circuit. Zero-state response means zero initial conditions. For the zero-state circuit shown earlier, zero initial conditions means looking at the circuit with zero inductor current at t < 0. You need to find the homogeneous and particular solutions to get the zero-state response.
Next, you have zero initial conditions and an input current of iN(t) = u(t), where u(t) is a unit step input.
When the step input u(t) = 0, the solution to the differential equation is the solution ih(t):
![]()
The inductor current ih(t) is the solution to the homogeneous first-order differential equation:
![]()
This solution is the general solution for the zero input. You find the constant c1 after finding the particular solution and applying the initial condition of no inductor current.
After time t = 0, a unit step input describes the transient inductor current. The inductor current for this step input is called the step response.
You find the particular solution ip(t) by setting the step input u(t) equal to 1. For a unit step input iN(t) = u(t), substitute u(t) = 1 into the differential equation:
![]()
The particular solution ip(t) is the solution for the differential equation when the input is a unit step u(t) = 1 after t = 0. Because u(t) = 1 (a constant) after time t = 0, assume a particular solution ip(t) is a constant IA.
Because the derivative of a constant is 0, the following is true:
![]()
Substitute ip(t) = IA into the first-order differential equation:

The particular solution eventually follows the form of the input because the zero-input (or free response) diminishes to 0 over time. You can generalize the result when the input step has strength IA or IAu(t).
You need to add the homogeneous solution ih(t) and the particular solution ip(t) to get the zero-state response:

At t = 0, the initial condition is 0 because this is a zero-state calculation. To find c1, apply iZS(0) = 0:

Solving for c1 gives you
C1 = -IASubstituting c1 into the zero-state response iZS(t), you wind up with