To understand string theory, you need to understand the meaning of the extra dimensions required. First, look at the concept of dimensions in a very general way, and the different approaches mathematicians have used to study 2- and 3-dimensional space.
Time is the fourth dimension. Then you can analyze the ways in which the extra dimensions may manifest in string theory and whether the extra dimensions are really necessary.
When looking in our world, it has three dimensions — up and down, left and right, back and forth. If you give a longitude, latitude, and an altitude, you can determine any location on Earth, for example.
Expanding on the idea of Cartesian geometry, you find that it’s possible to create a Cartesian grid in three dimensions as well as two, as shown in this figure. In such a grid, you can define an object called a vector, which has both a direction and a length. In 3-dimensional space, every vector is defined by three quantities.
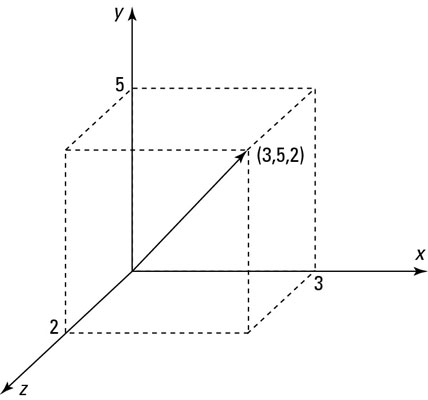
Vectors can, of course, exist in one, two, or more than three dimensions. (Technically, you can even have a zero-dimensional vector, although it will always have zero length and no direction. Mathematicians call such a case “trivial.”)
Treating space as containing a series of straight lines is probably one of the most basic operations that can take place within a space. One early field of mathematics that focuses on the study of vectors is called linear algebra, which allows you to analyze vectors and things called vector spaces of any dimensionality. (More advanced mathematics can cover vectors in more detail and extend into nonlinear situations.)
One of the major steps of working with vector spaces is to find the basis for the vector space, a way of defining how many vectors you need to define any point in the entire vector space. For example, a 5-dimensional space has a basis of five vectors. One way to look at superstring theory is to realize that the directions a string can move can only be described with a basis of ten distinct vectors, so the theory describes a 10-dimensional vector space.





