Predicting Gas Pressure Using the Ideal Gas Law

In physics, you can use the ideal gas law to predict the pressure of an ideal gas if you know how much gas you have, its temperature, and the volume you’ve enclosed it in.

For an ideal gas (at constant volume), pressure is directly proportional to temperature.

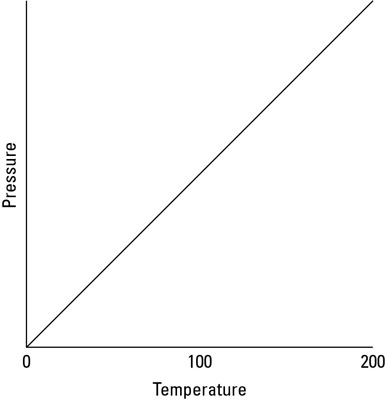
Here’s how the various factors affect pressure:

• Temperature. Experiments show that if you keep the volume constant and heat a gas, the pressure goes up linearly, as you see in the preceding figure. In other words, at a constant volume, where T is the temperature measured in kelvins and P is the pressure, the pressure is proportional to temperature:

  

• Volume. If you let the volume vary, you also find that the pressure is inversely proportional to the volume:

  

  For instance, if the volume of a gas doubles (while the temperature is held constant), its pressure is cut in half.

• Moles. When the volume and temperature of an ideal gas are constant, the pressure is proportional to the number of moles of gas you have — twice the amount of gas, twice the pressure. If the number of moles is n, then you can say the following:

  

  relates pressure, volume, number of moles, and temperature:

  PV = nRT

The unit of pressure is the pascal and the unit of volume is meters³, and they combine to give the joule; when the quantity of gas, n, is measured in moles and the temperature, T, is measured in kelvins, the units of the universal gas constant, R, are joules/mole-kelvin

You can also express the ideal gas law a little differently by using the total number of molecules, N, and Avogadro’s number, N_A:

The constant R/N_A is also called Boltzmann’s constant, k, and it has a value of

Using this constant, the ideal gas law becomes

PV = NkT

Say that you’re measuring a volume of 1 cubic meter filled with 600 moles of helium at room temperature, 27 degrees Celsius, which is very close to an ideal gas under these conditions. What’s the pressure of the gas? Using this form of the ideal gas law, PV = nRT, you can put P on one side by dividing by V. Now plug in the numbers, making sure you convert temperature to kelvins:

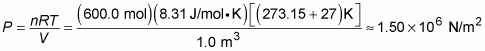
The pressure on all the walls of the container is

Notice the units of pressure here — newtons per square meter. The unit is used so commonly that it has its own name in the MKS (meter-kilogram-second) system: pascals, or Pa.

One pascal equals 1 newton per square meter, or

Atmospheric pressure is

which is 14.70 pounds per square inch. The pressure of 1 atmosphere is also given in torr on occasion, and 1.0 atmosphere = 760 torr.

In this example, you have a pressure of

which is about 15 atmospheres.