The first step in working with ramps of any kind is to resolve the forces that you're dealing with, and that means using vectors. For example, take a look at the cart in the figure; it's on an inclined plane, ready to roll.
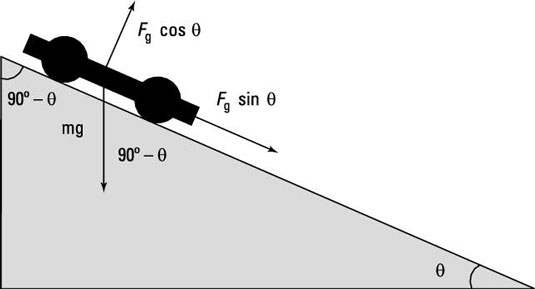
The force on the cart is the force due to gravity, Fg = mg. So how fast will the cart accelerate along the ramp? To get the answer, you should resolve the gravitational force — not in the horizontal and vertical directions, however, but along the ramp's inclined plane and perpendicular to that plane.
The reason you resolve the gravitational force in these directions is because the force along the plane provides the cart's acceleration while the force perpendicular to the rampdoes not. (When you start introducing friction into the picture, you'll see that the force of friction is proportional to the normal force — that is, it's proportional to the force with which the object going down the ramp presses against the ramp.)
Sample question
In the figure, what are the forces along the ramp and normal to the ramp?
The correct answer is

along the ramp,

normal (perpendicular to the ramp).
To resolve the vector Fg along the ramp, you can start by figuring out the angle between Fg and the ramp.
Here’s where your knowledge of triangles comes into play. Because you know that a triangle’s angles have to add up to 180 degrees, the angle between Fg and the ground is 90 degrees. The figure shows you that the ramp’s angle to the ground is theta, so you know that the angle between Fg and the ramp must be

The angle between Fg and the ramp is

So what’s the component of Fg along the ramp? Knowing the angle between Fg and the ramp, you can figure out the component of Fg along the ramp as usual:

3.Apply the following equation:

Notice that this makes sense because as theta goes to 0 degrees, the force along the ramp also goes to zero, and as theta goes to 90 degrees, the force along the ramp goes to Fg.
Solve for the normal force, Fn, perpendicular to the ramp:

The normal force, Fn, must exactly balance the component of the force of gravity perpendicular to the inclined plane. Apply the following equation:

Practice questions
Suppose that the cart in the figure has a mass of 1.0 kg and the angle theta = 30 degrees. What are the forces on the cart along and normal to the ramp?
Suppose that the cart in the figure has a mass of 3.0 kg and the angle theta = 45 degrees. What are the forces on the cart along and normal to the ramp?
You have a block of ice with a mass of 10.0 kg on a ramp at an angle of 23 degrees. What are the forces on the ice along and normal to the ramp?
You have a refrigerator with a mass of 1.00 x 102 kg on a ramp at an angle of 19 degrees. What are the forces on the refrigerator along and normal to the ramp?
Following are answers to the practice questions:
4.9 N along the ramp, 8.5 N normal to the ramp
1.You know that the forces on the cart are

along the ramp and

normal to the ramp.
2.Plug the numbers into Fg = mg: 1.0(9.8) = 9.8 N.
3.The force along the ramp is

4.The force normal to the ramp is

21 N along the ramp, 21 N normal to the ramp
1.The forces on the cart are

along the ramp and

normal to the ramp.
2.Plug the numbers into Fg = mg: 3.0(9.8) = 29 N.
3.The force along the ramp is

4.The force normal to the ramp is

38 N along the ramp, 90 N normal to the ramp
1.The forces on the ice are

along the ramp and

normal to the ramp.
2.Plug the numbers into Fg = mg: 10.0(9.8) = 98 N.
3.The force along the ramp is

4.The force normal to the ramp is

320 N along the ramp, 930 N normal to the ramp
The forces on the ice are

along the ramp and

normal to the ramp.
Plug the numbers into Fg = mg: (1.00 x 102)(9.8) = 980 N.
The force along the ramp is

The force normal to the ramp is






