Imagine that the product of one reaction serves as the reactant for another reaction. Now imagine that the product of the second reaction serves as the reactant for a third reaction. What you have is a set of coupled reactions, connected in series like the cars of a train:
Therefore,
You can think of these three reactions adding up to one big reaction
What is the overall enthalpy change associated with this reaction
Here's the good news:
Enthalpy changes are additive. But the good news gets even better. Imagine that you're trying to figure out the total enthalpy change for the following multistep reaction:
Here's a wrinkle: For technical reasons, you can't measure this enthalpy change
directly but must calculate it from tabulated values for
and
No problem, right? You simply look up the tabulated values and add them. But here's another wrinkle: when you look up the tabulated values, you find the following:
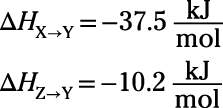
Gasp! You need
but you're provided only
Relax. The enthalpy change for a reaction has the same magnitude and opposite sign as the reverse reaction. So if
then
It really is that simple:
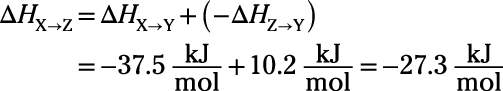
Thanks be to Hess.
Try an example. Calculate the reaction enthalpy for the following reaction:
Use the following data:
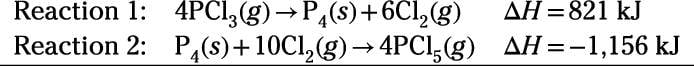
Reaction enthalpies are given for two reactions. Your task is to manipulate and add Reactions 1 and 2 so the sum is equivalent to the target reaction. First, reverse Reactions 1 and 2 to obtain Reactions
and
and add the two reactions. Identical species that appear on opposite sides of the equations cancel out (as occurs with species P4 and Cl2):
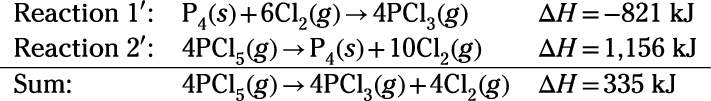
Finally, divide the sum by 4 to yield the target reaction equation:
So, the reaction enthalpy for the reaction is 83.8 kJ.

