Consider a satellite that orbits earth at an altitude of 750 miles. Earth has a radius of 3,950 miles. How far in any direction can the satellite's cameras see? The figure shows the satellite and the length of the camera's scope due to the curvature of earth.
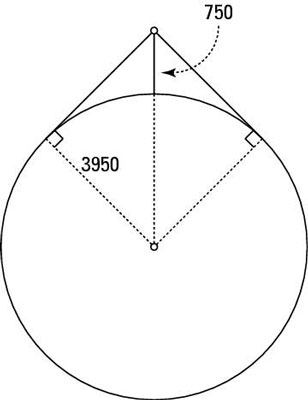
Identify the parts of the triangle that you can use to solve the problem.
Because a satellite's line of sight is tangent to the curvature of earth, and tangents to a circle form 90-degree angles with radii of the circle, you can see two right triangles in the figure.
The two sides of angle θ are the radius touching the tangent to the circle and the segment extending from the center of the circle up to the satellite. These sides are the hypotenuse and adjacent side of the right triangle with acute angle θ.
Determine which trig function to use.
The adjacent side and hypotenuse are part of the ratio for the cosine of θ.
Write the equation with the trig function; then input the measures that you know and solve for cos è.
The adjacent side measures 3,950 miles, and the hypotenuse is the sum of the radius and height of the satellite: 3,950 + 750 = 4,700 miles.
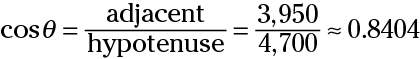
Determine the value of è.
Refer to the Appendix to find the angle whose cosine is closest to 0.8404. To the nearest degree, an angle of 33 degrees has this cosine.
Determine how much of earth's circumference is covered in either direction from the satellite.
The satellite’s line of sight goes 33 degrees in either direction, or 66 degrees total, which is 66/360 of the entire circumference (because all the way around would be 360 degrees). If the radius of Earth is 3,950 miles, then you can substitute that number into the equation for a circle’s circumference:
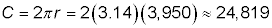
That’s the earth’s circumference. The distance that the satellite scans, then, is
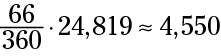
or about 4,550 miles in any direction.

