A big advantage of trig expressions and equations is that you can adjust them in so many ways to suit your needs. The basic reciprocal identities here are the ones people use most frequently.
Take a look at the first reciprocal identity and its counterpart:
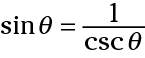
and
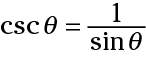
An alternate way of writing these identities uses an exponent of ‒1 rather than a fraction:
Note that the exponents apply to the entire function. These are not the inverse functions:
Secant, cosecant, and cotangent are technically the three reciprocal functions, but you can write identities to show their reciprocals, too. Next are the second reciprocal identity and its counterpart.
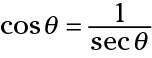
and
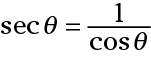
Again, another way of writing these is to use an exponent of –1. The parentheses are used to be sure you recognize that this is the reciprocal, not the inverse.
The tangent and its reciprocal at least have names that sound alike. The other two basic functions and their reciprocals (see the preceding equations) don’t seem to have names that are not as nicely related.
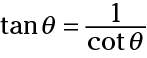
and
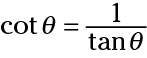
And, to finish off the alternate notation:




