The biggest advantage of using radians instead of degrees is that a radian is directly tied to a length — the length or distance around a circle, which is called its circumference. Using radians is very helpful when doing applications involving the length of an arc of a circle.
Radar scans a circular area that has a radius of 40 miles. In one second, it sweeps an arc of 60 degrees. What area does the radar cover in one second? In five seconds? The figure shows a sweep of 60 degrees.
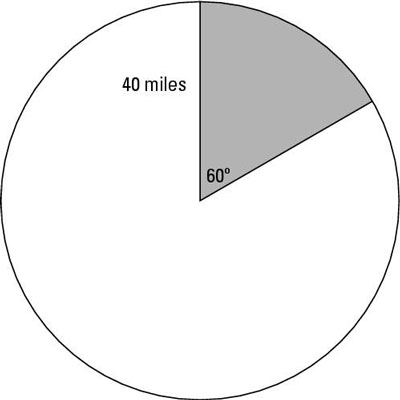
Here's how you solve this problem:
Find the area of the circle.
Use the formula for the area of a circle, A = πr2. Putting the 40 in for the radius, r, you get

Divide by the portion of the circle that the sweep covers.
The sweep of 60 degrees is only 1/6 of the entire circle, so you figure the area that the sweep covers by dividing the entire area by 6. The resulting area is 5,026.548/6 = 837.758 square miles, which is the area the radar scans in one second. To get the area covered in five seconds, multiply that result by 5 to get 4,188.790 square miles.
The preceding problem works out nicely, because the number of degrees is a convenient value — it's a fraction of the circle. But what if the number doesn't divide evenly into 360? For example, what if the radar sweeps an angle of 76 degrees in one second?
In general, if the angle is given in degrees, then the part of a circle that the angle sweeps is angle in degrees divided by 360. Take the fraction for that part of the circle and multiply it by the area, πr2. A fancy name for this part of a circle is sector.
Keep the following formulas in mind when you're trying to find the area of a sector:
Using degrees:

Using radians:

This formula comes from the following computation. That's why there's no pi in the result:
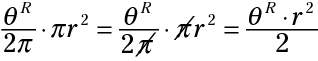
For example, to find the area of the radar sweep in the preceding example when the radar sweeps 76 degrees per second:
Put 76 in for the theta and 40 for the radius in the formula for the area of a sector.

Multiply and divide to simplify the answer.

To demonstrate this radar-sweep calculation if you're given measurements in radians, find the area of the radar sweep if the sweep is
radians (which is 60 degrees).
Put ð/3 in for the thetaR and 40 in for the radius.

Multiply and divide to simplify the answer.





