The sine function and any of its variations have two important characteristics: the amplitude and period of the curve. You can determine these characteristics by looking at either the graph of the function or its equation.
The amplitude of the sine function is the distance from the middle value or line running through the graph up to the highest point. In other words, the amplitude is half the distance from the lowest value to the highest value. In the sine and cosine equations, the amplitude is the coefficient (multiplier) of the sine or cosine. For example, the amplitude of y = sin x is 1. To change the amplitude, multiply the sine function by a number.
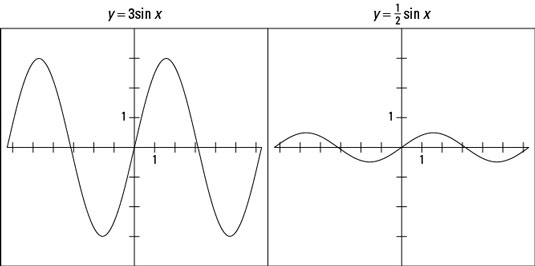
Take a look at the preceding figure, which shows the graphs of
As you can see, multiplying by a number greater than 1 makes the graph extend higher and lower. The amplitude of y = 3sin x is 3. Conversely, multiplying by a number smaller than 1 (but bigger than 0) makes the graph shrink in value — it doesn’t go up or down as far.





