Look at the graphs of the sine and cosine functions on the same coordinate axes, as shown in the following figure. The graph of the cosine is the darker curve; note how it’s shifted to the left of the sine curve.
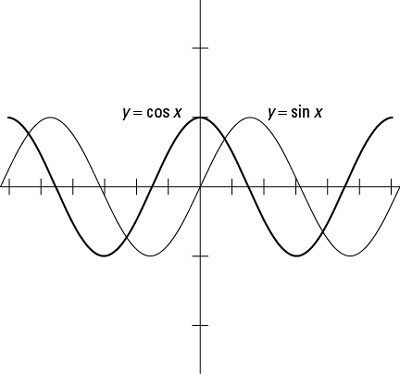The graphs of y = sin x and y = cos x on the same axesThe cofunction identities are as follows:
These identities show how the function values of the complementary angles in a right triangle are related. For example, cosθ = sin (90° – θ) means that if θ is equal to 25 degrees, then cos 25° = sin (90° – 25°) = sin 65°. This equation is a roundabout way of explaining why the graphs of sine and cosine are different by just a slide.
You probably noticed that these cofunction identities all use the difference of angles, but the slide of the sine function to the left was a sum. The shifted sine graph and the cosine graph are really equivalent — they become graphs of the same set of points. Here’s how to prove this statement.
You want to show that the sine function, slid 90 degrees to the left, is equal to the cosine function:
-
Replace cos x with its cofunction identity.
-
Apply the two identities for the sine of the sum and difference of two angles.
The two identities are
Substituting in the x’s and angles,
-
Simplify the terms by using the values of the functions.
So you see, the shifted sine graph is equal to the cosine graph.