In most cases, an algebraic equation is solvable only when one value is unknown — that is, when the equation has only one variable. In rare cases, you can solve an equation with two or more variables because one variable drops out. For example:
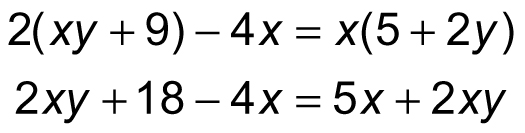
At this point, you can subtract 2xy from both sides of the equation:
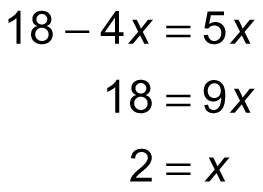
In most cases, however, an equation with two or more variables has multiple solutions. To solve it for specific values of two variables, you need an extra equation — that is, a system of two equations.
Substituting to solve a system of equations
When a system of equations is simple, the easiest way to solve it is by substitution. For example:
x + 3 = y
3x + y = 7
The first equation tells you that the value of y in terms of x is x + 3. To solve this system, substitute x + 3 for y in the second equation:
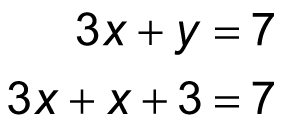
Now, this equation has only one variable, so you can solve it:
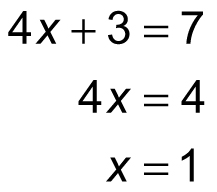
To find the value of y, substitute 1 for x back into either of the original equations — pick the easier of the two:
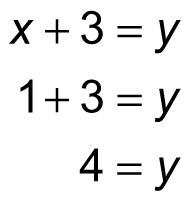
Therefore, in this system of equations, x = 1 and y = 4. Here’s another example using three variables:
x + y = z
x = 2 + y
3y = 2z
In this system, the second equation tells you that x is equal to 2 + y, so substitute 2 + y for x in the first equation and simplify:
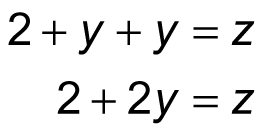
Now, you know that z equals 2 + 2y, so make this substitution for z in the third equation, then solve for y:
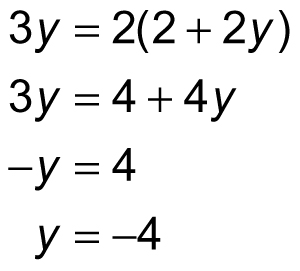
Thus, y = –4. Substitute this value back into the second equation:
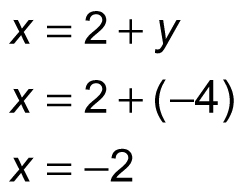
Thus, x = –2. You can also substitute –4 for y into the third equation to find the value of z:
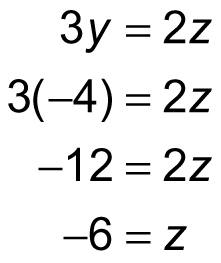
Therefore, in this system of equations, x = –2, y = –4, and z = –6.
Combining equations to solve a system of equations
Substitution works well for solving systems of equations when the equations are on the simple side. But when equations get more complicated, a better way to solve system is by combining equations. For example:
12x – 9y = 37
8x + 9y = 23
Neither equation in this system makes clear the value of one variable in terms of another, making substitution difficult. To solve this system more easily, add the two equations as follows:
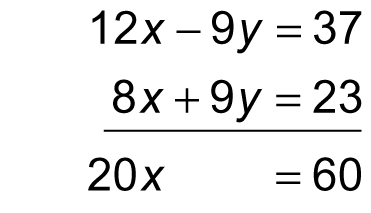
The resulting equation, 20x = 60 is very simple to solve:
x = 3
Now, substitute this value for x into either equation, whichever seems simpler:
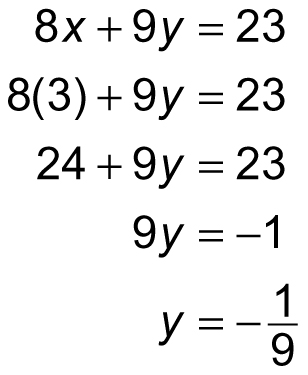
Therefore, in this system of equations, x = 3 and
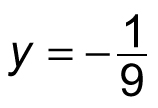
In some cases, when you use this method to solve a system of equations, you may need to multiply one or both equations by a constant in order to make one variable drop out of the system, as in the previous example. For example:
2x + 3y = 33
5x + 4y = 58
In this case, adding or subtracting the two equations won’t make one variable drop out. So, you want to target one variable that you’d like to see drop out of the two equations when they’re either added or subtracted. To make the x variable drop out, first multiply the first equation by 5, which is the x coefficient in the second equation:
10x + 15y = 165
5x + 4y = 58
Next, multiply the second equation by 2, which is the x coefficient in the first equation:
10x + 15y = 165
10x + 8y = 116
Notice now that the two equations share the term 10x. So, you can subtract the first equation minus the second as follows:

The resulting equation, 7y = 49, solves easily as follows:
y = 7
To solve for x, substitute 7 for y into whichever of the original equations seems easier to work with:
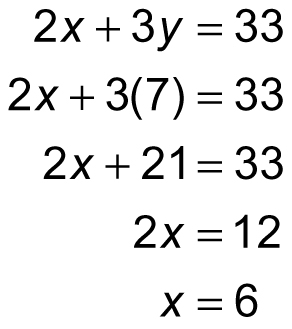
Therefore, in this system of equations, x = 6 and y = 7.





