Unlike geometric series and p-series, a power series often converges or diverges based on its x value. This leads to a new concept when dealing with power series: the interval of convergence.
The interval of convergence for a power series is the set of x values for which that series converges.
The interval of convergence is never empty
Every power series converges for some value of x. That is, the interval of convergence for a power series is never the empty set.
Although this fact has useful implications, it’s actually pretty much a no-brainer. For example, take a look at the following power series:
When x = 0, this series evaluates to 1 + 0 + 0 + 0 + ..., so it obviously converges to 1. Similarly, take a peek at this power series:
This time, when x = –5, the series converges to 0, just as trivially as the last example.
Note that in both of these examples, the series converges trivially at x = a for a power series centered at a.
Three possibilities for the interval of convergence
Three possibilities exist for the interval of convergence of any power series:
The series converges only when x = a.
The series converges on some interval (open or closed at either end) centered at a.
The series converges for all real values of x.
For example, suppose that you want to find the interval of convergence for:
This power series is centered at 0, so it converges when x = 0. Using the ratio test, you can find out whether it converges for any other values of x. To start out, set up the following limit:
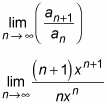
To evaluate this limit, start out by canceling xn in the numerator and denominator:
Next, distribute to remove the parentheses in the numerator:
As it stands, this limit is of the form
so apply L’Hopital’s Rule, differentiating over the variable n:
From this result, the ratio test tells you that the series:
Converges when –1 x
Diverges when x x > 1
May converge or diverge when x = 1 and x = –1
Fortunately, it’s easy to see what happens in these two remaining cases. Here’s what the series looks like when x = 1:
Clearly, the series diverges. Similarly, here’s what it looks like when x = –1:
This alternating series swings wildly between negative and positive values, so it also diverges.
As a final example, suppose that you want to find the interval of convergence for the following series:
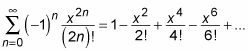
This series is centered at 0, so it converges when x = 0. The real question is whether it converges for other values of x. Because this is an alternating series, you apply the ratio test to the positive version of it to see whether you can show that it’s absolutely convergent:
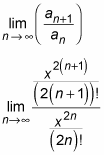
First off, you want to simplify this a bit:
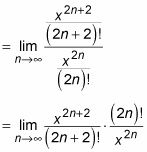
Next, you expand out the exponents and factorials:
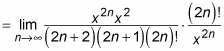
At this point, a lot of canceling is possible:
This time, the limit falls between –1 and 1 for all values of x. This result tells you that the series converges absolutely for all values of x, so the alternating series also converges for all values of x.





