Learn the method of undetermined coefficients to work out nonhomogeneous differential equations.
Classifying differential equations by order
The most common classification of differential equations is based on order. The order of a differential equation simply is the order of its highest derivative. You can have first-, second-, and higher-order differential equations.
First–order differential equations involve derivatives of the first order, such as in this example:
![]()
Second–order differential equations involve derivatives of the second order, such as in these examples:
![]()
Higher–order differential equations are those involving derivatives higher than the second order (big surprise on that clever name!). Differential equations of all orders can use the y‘ notation, like this:

Distinguishing among linear, separable, and exact differential equations
You can distinguish among linear, separable, and exact differential equations if you know what to look for. Keep in mind that you may need to reshuffle an equation to identify it.
Linear differential equations involve only derivatives of y and terms of y to the first power, not raised to any higher power. (Note: This is the power the derivative is raised to, not the order of the derivative.) For example, this is a linear differential equation because it contains only derivatives raised to the first power:
![]()
Separable differential equations can be written so that all terms in x and all terms in y appear on opposite sides of the equation. Here’s an example:
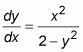
which can be written like this with a little reshuffling:
![]()
Exact differential equations are those where you can find a function whose partial derivatives correspond to the terms in a given differential equation.
Defining homogeneous and nonhomogeneous differential equations
In order to identify a nonhomogeneous differential equation, you first need to know what a homogeneous differential equation looks like. You also often need to solve one before you can solve the other.
Homogeneous differential equations involve only derivatives of y and terms involving y, and they’re set to 0, as in this equation:
![]()
Nonhomogeneous differential equations are the same as homogeneous differential equations, except they can have terms involving only x (and constants) on the right side, as in this equation:
![]()
You also can write nonhomogeneous differential equations in this format: y” + p(x)y‘ + q(x)y = g(x). The general solution of this nonhomogeneous differential equation is
![]()
In this solution, c1y1(x) + c2y2(x) is the general solution of the corresponding homogeneous differential equation:
![]()
And yp(x) is a specific solution to the nonhomogeneous equation.
Using the method of undetermined coefficients
If you need to find particular solutions to nonhomogeneous differential equations, then you can start with the method of undetermined coefficients. Suppose you face the following nonhomogeneous differential equation:
![]()
The method of undetermined coefficients notes that when you find a candidate solution, y, and plug it into the left-hand side of the equation, you end up with g(x). Because g(x) is only a function of x, you can often guess the form of yp(x), up to arbitrary coefficients, and then solve for those coefficients by plugging yp(x) into the differential equation.
This method works because you’re dealing only with g(x), and the form of g(x) can often tell you what a particular solution looks like.





